��Ŀ����
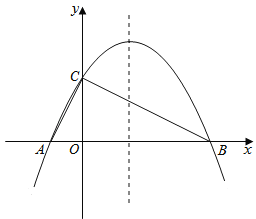
����Ŀ����12�֣���ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�
��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�![]() ����P��ֱ��BC�·��������ϵ�һ�����㣮
����P��ֱ��BC�·��������ϵ�һ�����㣮
��1������κ�������ʽ��
��2������PO��PC��������POC��y����ۣ��õ��ı���![]() .�Ƿ���ڵ�P��ʹ�ı���
.�Ƿ���ڵ�P��ʹ�ı���![]() Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC��������.


���𰸡���1��![]() ��2��
��2��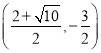 ��3��
��3��![]() ��
�� ![]() .
.
�������������������1�����ô���ϵ��������B��C��������������ߵĽ���ʽ�м�����ô���ϵ����ֵ������Ϳɵý⣻
��2����PE��CO��E���������εĶԽ����ഹֱƽ�֣����ı���POP��CΪ���Σ���ôP�����OC�Ĵ�ֱƽ�����ϣ��ݴˣ������ֱ��PE�Ľ���ʽ�����������ߵĽ���ʽ���������P������ꣻ
��3��������ABC�����Ϊ��ֵ�����ı���ABPC��������ʱ����BPC��������P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ���������BPC��������ɴˣ��ɵõ������ı���ACPB�������P�������ĺ�����ϵʽ���ٸ��ݺ��������ʼ�������ı���ABPC������������Ӧ��P������.
�����������1����B��C������������![]() ����
����![]()
��֮����![]()
���Զ��κ����Ľ���ʽΪ![]() .
.
��2����ͼ1�������������ϴ��ڵ�P��ʹ�ı���![]() Ϊ���Σ�����
Ϊ���Σ�����![]() ��CO�ڵ�E��
��CO�ڵ�E��
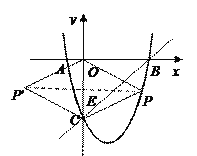
���ı���![]() Ϊ���Σ�
����
��PC=PO����PE��CO��
��OE=EC=![]() ����P���������Ϊ
����P���������Ϊ![]()
��![]() =
=![]() ����
����
![]() ���������⣬��ȥ��
���������⣬��ȥ��
���Դ��������ĵ㣬��ʱP�������Ϊ��![]() ��
�� ![]() ��.
��.
��3����ͼ2������PO����PM��x��M��PN��y��N����P������Ϊ��x�� ![]() ����
����

��![]() =0���õ�A����Ϊ����1��0��.
=0���õ�A����Ϊ����1��0��.
��AO=1��OC=3�� OB=3��P��=![]() ��PN��x��
��PN��x��
��S�ı���ABPC=![]() +
+![]() +
+![]()
=![]() AO��OC+
AO��OC+![]() OB��PM+
OB��PM+![]() OC��PN
OC��PN
=![]() ��1��3+
��1��3+![]() ��3��(
��3��(![]() )+
)+![]() ��3��x
��3��x
=![]()
=![]() .
.
��֪����x=![]() ʱ���ı���ABPC��������ʱP������Ϊ��
ʱ���ı���ABPC��������ʱP������Ϊ��![]() ��
�� ![]() �����ı���ABPC��������Ϊ
�����ı���ABPC��������Ϊ![]() .
.