题目内容
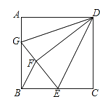
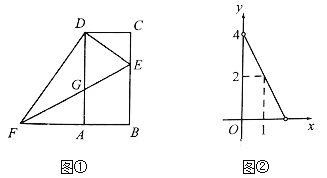
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
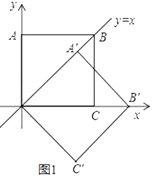
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
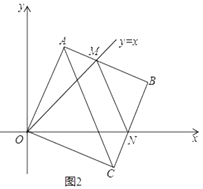
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
【答案】(1)![]() ,
,![]() ;(2)①AM+CN=MN,理由见解析;②
;(2)①AM+CN=MN,理由见解析;②![]() .
.
【解析】
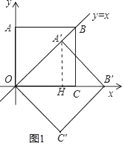
(1)如图1中,作A′H⊥OB′于H.易知△OA′H是等腰直角三角形,点B′在x轴上,由此即可解决问题;
(2)①结论:AM+CN=MN;延长BA交y轴于E点,由△OAE≌△OCN(ASA),推出△OME≌△OMN(SAS),可得MN=ME=AM+AE,推出MN=AM+CN;
②利用①中结论,求出BM、BN、MN,根据△BMN的内切圆半径![]() 计算即可.
计算即可.
解:(1)如图1中,作A′H⊥OB′于H.
∵四边形ABCD是正方形,
∴OA=OC=BC=AB=2,∠BOC=45°=45,![]() ,
,
∵OA′=2,
∴![]() ,
,
∴![]() ,
,
∵旋转角为45°,
∴B′在x轴上,
∴![]() ,
,
故答案为![]() ,
,![]() ;
;
(2)①结论:AM+CN=MN;
理由:延长BA交y轴于E点,
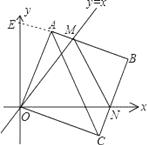
则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,
∴∠AOE=∠CON,
又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN,
在△OAE和△OCN中,
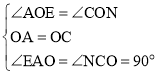 ,
,
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN,
在△OME和△OMN中
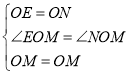 ,
,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
②∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,
∴BM=BN,∵BA=BC,
∴AM=NC,
设AM=NC=a,则MN=2a,
在Rt△BMN中,(2a)2=(2﹣a)2+(2﹣a)2,
解得![]() 或
或![]() (舍弃),
(舍弃),
∴![]() ,
,![]() ,
,
∴△BMN的内切圆半径![]() .
.

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()