МвДҝДЪИЭ
ЎҫМвДҝЎҝФД¶БПВБРІДБПЈә
ІДБП1ЈәФЪҙҰАн·ЦКэәН·ЦКҪОКМвКұЈ¬УРКұУЙУЪ·ЦЧУұИ·ЦДёҙ󣬻тХЯ·ЦЧУөДҙОКэёЯУЪ·ЦДёөДҙОКэЈ¬ФЪКөјКФЛЛгКұНщНщДС¶ИұИҪПҙуЈ¬ХвКұОТГЗҝЙТФҪ«јЩ·ЦКэ(·ЦКҪ)Ір·ЦіЙТ»ёцХыКэ(ХыКҪ)УлТ»ёцХж·ЦКэ(КҪ)өДәН(Іо)өДРОКҪЈ¬НЁ№э¶ФјтөҘКҪөД·ЦОцАҙҪвҫцОКМвЈ¬ОТГЗіЖЦ®ОӘ·ЦАлХыКэ·ЁЈ®ҙЛ·ЁФЪҙҰАн·ЦКҪ»тХыіэОКМвКұЖДОӘУРР§Ј®
АэЈәҪ«·ЦКҪ![]() Ір·ЦіЙТ»ёцХыКҪУлТ»ёц·ЦКҪ(·ЦЧУОӘХыКэ)өДәНөДРОКҪЈ®
Ір·ЦіЙТ»ёцХыКҪУлТ»ёц·ЦКҪ(·ЦЧУОӘХыКэ)өДәНөДРОКҪЈ®
ҪвЈәЙиx+2=tЈ¬Фтx=t©Ғ2Ј®
ЎаФӯКҪ=![]()
Ўа![]()
ХвСщЈ¬·ЦКҪ![]() ҫНІр·ЦіЙТ»ёцХыКҪ(x©Ғ5)УлТ»ёц·ЦКҪ
ҫНІр·ЦіЙТ»ёцХыКҪ(x©Ғ5)УлТ»ёц·ЦКҪ![]() өДәНөДРОКҪЈ®
өДәНөДРОКҪЈ®
ёщҫЭТФЙПФД¶БІДБП»ШҙрПВБРОКМвЈә
(1)Ҫ«·ЦКҪ![]() Ір·ЦіЙТ»ёцХыКҪУлТ»ёц·ЦЧУОӘХыКэөД·ЦКҪөДәНөДРОКҪЈ¬ФтҪб№ыОӘЎЎ ЎЎЈ»
Ір·ЦіЙТ»ёцХыКҪУлТ»ёц·ЦЧУОӘХыКэөД·ЦКҪөДәНөДРОКҪЈ¬ФтҪб№ыОӘЎЎ ЎЎЈ»
(2)ТСЦӘ·ЦКҪ![]() өДЦөОӘХыКэЈ¬ЗуХыКэxөДЦөЈ»
өДЦөОӘХыКэЈ¬ЗуХыКэxөДЦөЈ»
Ўҫҙр°ёЎҝ(1) x+![]() Ј»(2) 0»т1Ј»
Ј»(2) 0»т1Ј»
ЎҫҪвОцЎҝ
ЈЁ1Ј©Йиx+1=tЈ¬Фтx=t©Ғ1Ј¬Ҫ«ФӯКҪұдРООӘә¬tөДКҪЧУЈ¬ФЩ»ҜјтОӘТ»ёцХыКҪУлТ»ёц·ЦКҪөДәНРОКҪЈ¬ФЩҪ«t»№ФӯОӘxјҙҝЙЈ»
ЈЁ2Ј©ПИҪ«·ЦКҪЧӘ»ҜОӘТ»ёцХыКҪәНТ»ёц·ЦКҪөДәНөДРОКҪЈ¬И»әуФЩМЦВЫК№өГ·ЦКҪІҝ·ЦТІКЗХыКҪКұxөДЦөЈ®
ҪвЈә(1)Йиx+1=tЈ¬
Ўаx=t©Ғ1Ј¬
ЎаФӯКҪ=![]()
=![]()
=t+![]() ©Ғ1
©Ғ1
=x+1+![]() ©Ғ1
©Ғ1
=x+![]() Ј»
Ј»
(2)Йи2x©Ғ1=tЈ¬
Ўаx=![]() Ј¬
Ј¬
ЎаФӯКҪ=![]()
=![]()
=t+![]() ©Ғ3Ј¬
©Ғ3Ј¬
=2x©Ғ1+![]() ©Ғ3
©Ғ3
=2x+![]() ©Ғ4
©Ғ4
өұ2x©Ғ1=ЎА1»тЎА2»тЎА4КұЈ¬ёГ·ЦКҪөДЦөОӘХыКэЈ¬
ЎЯxКЗХыКэЈ¬
Ўаx=0»т1Ј»

ЎҫМвДҝЎҝРЎНхДіФВКЦ»ъ»°·СЦРөДёчПо·СУГНіјЖЗйҝцјыПВБРНјұнЈ¬ЗлДгёщҫЭНјұнРЕПўНкіЙПВБРёчМвЈә
ПоДҝ | ФВ№ҰДЬ·С | »щұҫ»°·С | іӨНҫ»°·С | ¶МРЕ·С |
Ҫр¶о/ФӘ | 5 | Ўш | Ўш | 25 |
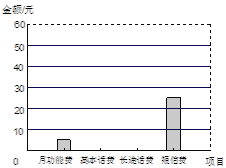
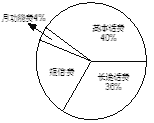
ЈЁ1Ј©ёГФВРЎНхКЦ»ъ»°·С№ІУР¶аЙЩФӘЈҝ
ЈЁ2Ј©ЙИРОНіјЖНјЦРЈ¬ұнКҫ¶МРЕ·СөДЙИРОөДФІРДҪЗОӘ¶аЙЩ¶ИЈҝ
ЈЁ3Ј©ЗлҪ«ұнёсІ№ідНкХыЈ»
ЈЁ4Ј©ЗлҪ«МхРОНіјЖНјІ№ідНкХыЈ®
ЎҫМвДҝЎҝ¶юҙОәҜКэ![]() ЈЁ
ЈЁ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘіЈКэЈ¬ЗТ
ОӘіЈКэЈ¬ЗТ![]() Ј©ЦРөД
Ј©ЦРөД![]() Ул
Ул![]() өДІҝ·Ц¶ФУҰЦөИзПВұнЈә
өДІҝ·Ц¶ФУҰЦөИзПВұнЈә
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТФПВҪбВЫЈә
ўЩ¶юҙОәҜКэ![]() УРЧоРЎЦөОӘ
УРЧоРЎЦөОӘ![]() Ј»
Ј»
ўЪөұ![]() КұЈ¬
КұЈ¬![]() Лж
Лж![]() өДФцҙу¶шФцҙуЈ»
өДФцҙу¶шФцҙуЈ»
ўЫ¶юҙОәҜКэ![]() өДНјПуУл
өДНјПуУл![]() ЦбЦ»УРТ»ёцҪ»өгЈ»
ЦбЦ»УРТ»ёцҪ»өгЈ»
ўЬөұ![]() КұЈ¬
КұЈ¬![]() .
.
ЖдЦРХэИ·өДҪбВЫУРЈЁ Ј©ёц
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()