��Ŀ����
����Ŀ����֪����ͼ���ڳ�����ABCD�У�AB=4��AD=6���ӳ�BC����E��ʹCE=3������DE��
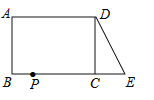
��1��DE�ij��� ����
��2������P�ӵ�B��������ÿ��1����λ���ٶ���BC��CD��DA���յ�A�˶������P�˶���ʱ��Ϊt�룬��tΪ��ֵʱ����ABP�͡�DCEȫ�ȣ�
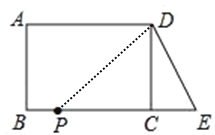
��3��������P�ӵ�B��������ÿ��1����λ���ٶȽ�����BE���յ�E�˶�������DP�����P�˶���ʱ��Ϊt�룬�Ƿ����t��ʹ��PDEΪ���������Σ������ڣ���ֱ��д��t��ֵ������˵�����ɣ�
���𰸡���1��5����2����tΪ3���13��ʱ����ABP����DCEȫ�ȣ���3��t��ֵΪ3��4��![]() ��
��
��������
��1�����ݾ��ε����ʿɵ�CD��4�����ݹ��ɶ�������DE�ij���
��2������ABP����DCEȫ�ȣ��ɵ�AP��CE��3��BP��CE��3������ʱ�䣽·�����ٶȣ�����t��ֵ��
��3����PD��DE��PE��DE��PD��PE����������ۣ��ֱ����õ��������ε����ʺ��ɶ������BP�����ɵõ�t��ֵ��
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AB��CD��4��AD��BC��6��CD��BC��
��Rt��DCE��DE��![]() ��5��
��5��
�ʴ�Ϊ 5��
��2������ABP����DCEȫ�ȣ���BP��CE��AP��CE��
��BP��CE��3ʱ����t��![]() ��3�룬
��3�룬
��AP��CE��3ʱ����t��![]() ��13�룬
��13�룬
�൱tΪ3���13��ʱ����ABP����DCEȫ�ȣ�
��3������PDE������������PD��DE��PE��DE��PD��PE��
��PD��DEʱ��
��PD��DE��DC��BE��
��PC��CE��3��
��BP��BCPC��3��
��t��![]() ��3��
��3��
��PE��DE��5ʱ��
��BP��BEPE��
��BP��6+35��4��
��t��![]() ��4��
��4��
��PD��PEʱ��
��PE��PC��CE��3��PC��
��PD��3��PC��
��Rt��PDC��PD2��CD2��PC2��
�ࣨ3��PC��2��16��PC2��
��PC��![]() ��
��
��BP��BCPC��![]() ��
��
�� ��
��
����������t��ֵΪ3��4��![]() ��
��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�



