题目内容
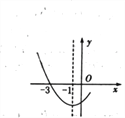
【题目】如图是二次函数![]() 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是抛物线上两点,则y1>y2,其中说法正确的有( )
是抛物线上两点,则y1>y2,其中说法正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】试题分析:根据图象分别求出a、b、c的符号,即可判断①,根据对称轴求出b=2a,即可判断②,把x=2代入二次函数的解析式,再根据图象即可判断③,求出点(-5,y1)关于直线x=-1的对称点的坐标,根据对称轴即可判断y1和y2的大小.
解:∵抛物线开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=1,
∴![]() =1,
=1,
∴b=2a>0,
∴abc<0,
∴①正确;
∵b=2a,
∴2ab=0,
∴②正确;
把x=2代入y=ax2+bx+c得:y=4a+2b+c,
从图象可知,当x=2时y>0,
即4a+2b+c>0,
∴③错误;
∵(5,y1)关于直线x=1的对称点的坐标是(3,y1),
又∵当x>1时,y随x的增大而增大,3>![]() ,
,
∴y1>y2,
∴④正确;
即正确的有3个,
故选B.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目