题目内容
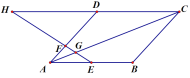
【题目】如图,已知![]() 是
是![]() 的直径,过
的直径,过![]() 点作
点作![]() ,交弦
,交弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且使
,且使![]() .
.
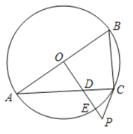
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)PE= 4﹣2 ![]() .
.
【解析】
(1)连接OC,由在计算的圆周角为直角可得∠ACB=90°,根据等腰三角形的性质及已知条件易得∠BCO=∠ACP,由此可得∠OCP=90°,即可证得PC是⊙O的切线;(2)在Rt△OCP中,求得OC=2 ![]() ,OP=4,由此即可求得PE的长.
,OP=4,由此即可求得PE的长.
(1)证明:连接OC,
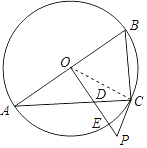
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCO+∠ACO=90°,
∵OC=OB,
∴∠B=∠BCO,
∵∠PCA=∠ABC,
∴∠BCO=∠ACP,
∴∠ACP+∠OCA=90°,
∴∠OCP=90°,
∴PC是⊙O的切线;
(2)解:∵∠P=60°,PC=2,∠PCO=90°,
∴OC=2 ![]() ,OP=2PC=4,
,OP=2PC=4,
∴PE=OP﹣OE=OP﹣OC=4﹣2 ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了进一步了解八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图.
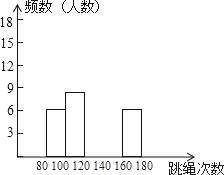
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?