题目内容
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.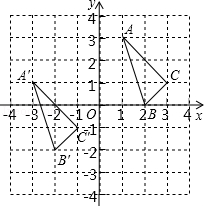
(1)分别写出下列各点的坐标:A′; B′;C′;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为;
(4)求△ABC的面积.
【答案】
(1)(﹣3,1);(﹣2,﹣2);(﹣1,﹣1)
(2)先向左平移4个单位,再向下平移2个单位
(3)(a﹣4,b﹣2)
(4)
解:△ABC的面积=2×3﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×1×1﹣
×1×1﹣ ![]() ×2×2
×2×2
=6﹣1.5﹣0.5﹣2
=2
【解析】解:(1)A′(﹣3,1); B′(﹣2,﹣2);C′(﹣1,﹣1);(2)先向左平移4个单位,再向下平移2个单位;
或:先向下平移2个单位,再向左平移4个单位;(3)P′(a﹣4,b﹣2);
(1)根据平面直角坐标系写出各点的坐标即可;(2)根据对应点A、A′的变化写出平移方法即可;(3)根据平移规律逆向写出点P′的坐标;(4)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.

练习册系列答案
相关题目
【题目】春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2 . 
(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:
x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
观察表中数据,写出y随x变化的一个特征: .