题目内容
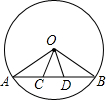
已知：如图，在⊙O中M，N分别为弦AB，CD的中点，AB=CD，AB不平行于CD．
求证：∠AMN=∠CNM．
求证：∠AMN=∠CNM．
证明：连接OM，ON，AO，OC，如图所示，
∵M、N分别为AB、CD的中点，
∴OM⊥AB，ON⊥CD，
又AB=CD，∴AM=CN，
在Rt△AOM和Rt△CON中，
∵
，
∴Rt△AOM≌Rt△CON（HL），
∴OM=ON，
∴∠OMN=∠ONM，
∴∠AMO+∠OMN=∠CNO+∠ONM，即∠AMN=∠CNM．
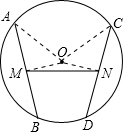
∵M、N分别为AB、CD的中点，
∴OM⊥AB，ON⊥CD，
又AB=CD，∴AM=CN，
在Rt△AOM和Rt△CON中，
∵
|
∴Rt△AOM≌Rt△CON（HL），
∴OM=ON，
∴∠OMN=∠ONM，
∴∠AMO+∠OMN=∠CNO+∠ONM，即∠AMN=∠CNM．
练习册系列答案
特高级教师点拨系列答案
相关题目
