题目内容
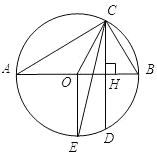
如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD=4
,求∠BAC的度数;
(2)若点E为
的中点,连接OE,CE.求证:CE平分∠OCD;
(3)在(1)的条件下,圆周上到直线AC距离为3的点有多少个?并说明理由.
(1)如果⊙O的半径为4,CD=4
| 3 |
(2)若点E为
 |
| ADB |
(3)在(1)的条件下,圆周上到直线AC距离为3的点有多少个?并说明理由.

(1)∵AB为⊙O的直径,CD⊥AB
∴CH=
CD=2
(1分)
在Rt△COH中,sin∠COH=
=
=
,
∴∠COH=60° (2分)
∴∠BAC=
∠COH=30°;(3分)
(2)证明:∵点E是
的中点
∴OE⊥AB (4分)
又∵CD⊥AB,
∴OE∥CD
∴∠ECD=∠OEC (5分)
又∵∠OEC=∠OCE
∴∠OCE=∠DCE (6分)
∴CE平分∠OCD;(6分)
(3)圆周上到直线AC的距离为3的点有2个. (8分)
因为圆弧
上的点到直线AC的最大距离为2,
上的点到直线AC的最大距离为6,2<3<6,根据圆的轴
对称性,
到直线AC距离为3的点有2个. (10分)

∴CH=
| 1 |
| 2 |
| 3 |
在Rt△COH中,sin∠COH=
| CH |
| OC |
2
| ||
| 4 |
| ||
| 2 |
∴∠COH=60° (2分)
∴∠BAC=
| 1 |
| 2 |
(2)证明:∵点E是
 |
| ADB |
∴OE⊥AB (4分)
又∵CD⊥AB,
∴OE∥CD
∴∠ECD=∠OEC (5分)
又∵∠OEC=∠OCE
∴∠OCE=∠DCE (6分)
∴CE平分∠OCD;(6分)
(3)圆周上到直线AC的距离为3的点有2个. (8分)
因为圆弧
 |
| AC |
 |
| ADC |
对称性,
 |
| ADC |


练习册系列答案
相关题目






