题目内容
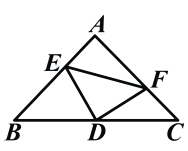
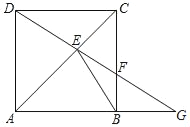
【题目】如图，四边形ABCD是矩形，E是对角线AC上的一点，EB=ED且∠ABE=∠ADE．
（1）求证：四边形ABCD是正方形；
（2）延长DE交BC于点F，交AB的延长线于点G，求证：EFAG=BCBE．
【答案】（1）（2）见解析
【解析】分析：（1）根据邻边相等的矩形是正方形即可证明；
（2）由AD∥BC，推出
，同理
，由DE=BE，四边形ABCD是正方形，推出BC=DC，可得
解决问题；
详解：（1）证明：连接BD．
∵EB=ED，
∴∠EBD=∠EDB，
∵∠ABE=∠ADE，
∴∠ABD=∠ADB，
∴AB=AD，
∵四边形ABCD是矩形，
∴四边形ABCD是正方形．
（2）证明：∵四边形ABCD是矩形
∴AD∥BC，
∴，
同理，
∵DE=BE，
∵四边形ABCD是正方形，
∴BC=DC，
∴，
∴EFAG=BCBE．
【题目】随着信息技术的高速发展，计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣，老师把甲、乙两组各有10名学生，进行电脑汉字输入速度比赛，各组参赛学生每分钟输入汉字个数统计如下表：
输入汉字（个） | 132 | 133 | 134 | 135 | 136 | 137 |
甲组人数（人） | 1 | 0 | 1 | 5 | 2 | 1 |
乙组人数（人） | 0 | 1 | 4 | 1 | 2 | 2 |
（1）请你填写下表中甲班同学的相关数据.
组 | 众数 | 中位数 | 平均数（ | 方差（ |
甲组 | ||||
乙组 | 134 | 134.5 | 135 | 1.8 |
（2）若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？
（3）请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）.
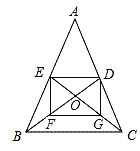
【题目】如图，正方形ABCD内部有若干个点，用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形（互相不重叠）：
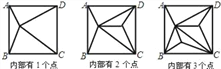
（1）填写下表：
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
（2）原正方形能否被分割成2008个三角形？若能，求此时正方形ABCD内部有多少个点？若不能，请说明理由．
