题目内容
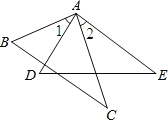
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的动点且BD=CE,连接AD与BE相交于点F,连接CF,下列结论:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,则FA=FB=FC;④∠AFC=90°,则AF=3BF,其中正确的结论共有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据等边三角形的性质可得∠C=∠ABC=60°,AB=BC,利用SAS可证明△ABD≌△BCE,可判定①正确;根据全等三角形的性质可得∠BAD=∠EBC,利用三角形外角性质可得∠AFE=∠BAD+∠ABE=∠ABC=60°,根据平角的定义可得∠AFB=120°,可判定②正确;由BD=CD,BD=CE可得点D、E为BC、AC的中点,根据等边三角形的性质可得AD、BE是BC、AC的垂直平分线,根据垂直平分线的性质可判定③正确;过点A作AG⊥BE于G,利用SAS可证明△ABE≌△ADC,根据全等三角形对应边上的高对应相等可得AG=CF,利用HL可证明△ABG≌△ACF,可得AF=BG,由∠AFE=60°可得∠FAG=30°,根据含30°角的直角三角形的性质可得AF=2FG,可得AF=BG=2FG=2BF,即可判定④错误.综上即可得答案.
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,
在△ABD和△ACE中, ,
,
∴△ABD≌△BCE,故①正确,
∴∠BAD=∠CBE,
∴∠AFE=∠BAD+∠ABE=∠CBE+∠ABE=∠ABC=60°,
∴∠AFB=180°-∠AFE=120°,故②正确,
∵BD=CD,BD=CE,
∴点D、E为BC、AC的中点,
∵△ABC是等边三角形,
∴BE、AD是BC、AC的垂直平分线,
∴FA=FB=FC,故③正确,
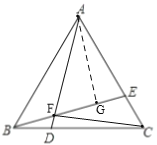
过点A作AG⊥BE于G,
∵BD=CE,BC=AC,
∴CD=AE,
在△ABE和△ADC中, ,
,
∴△ABE≌△ADC,
∵∠AFC=90°,AG⊥BE,
∴AG、CF是BE和AD边上的高,
∴AG=CF,
在△ABG和△ACF中,![]() ,
,
∴△ABG≌△ACF,
∴AF=BG,
∵AG⊥BE,∠AFE=60°,
∴∠FAG=30°,
∴AF=2FG,
∴BG=2FG,
∴BF=FG,
∴AF=2BF,故④错误,
综上所述:正确的结论有①②③,共3个,
故选C.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
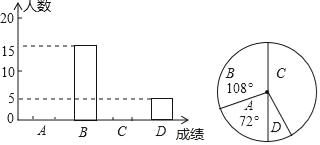
小学能力测试卷系列答案【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?