题目内容
【题目】如图.已知在平面直角坐标系中.点 A(0,m),点 B(n,0),D(2m,n),且 m、n 满足(m﹣2)2+![]() =0,将线段AB向左平移,使点B与点 O重合,点C与点A对应.
=0,将线段AB向左平移,使点B与点 O重合,点C与点A对应.
(1)求点C、D的坐标;
(2)连接CD,动点P从点O出发,以每秒1个单位的速度,沿射线OB方向运动,设点P运动时间为t秒,是否存在某一时刻,使 SPCD=4SAOB,若存在,请求出t值,并写出P点坐标;若不存在,请说明理由.
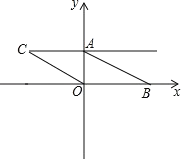
【答案】(1)点C的坐标为(﹣4,2);(2)P点坐标为(4,0).
【解析】
(1)由(m﹣2)2+![]() =0,得m=2,n=4,则A(0,2),B(4,0),D(4,4),
=0,得m=2,n=4,则A(0,2),B(4,0),D(4,4),
再由平移的性质可得点C的坐标为(﹣4,2);
(2)根据题意得[4﹣(﹣4)+t﹣(﹣4)]×4÷2﹣[4﹣(﹣4)]×(4﹣2)÷2﹣[t﹣(﹣4)]×2÷2,解得t=4,则P点坐标为(4,0).
(1)∵(m﹣2)2+![]() =0,
=0,
∴m﹣2=0,n﹣4=0,
解得m=2,n=4,
∴A(0,2),B(4,0),D(4,4),
∵将线段AB向左平移,使点B与点O重合,点C与点A对应,
∴点C的坐标为(﹣4,2);
(2)存在.
如果SPCD=4SAOB,则有:
[4﹣(﹣4)+t﹣(﹣4)]×4÷2﹣[4﹣(﹣4)]×(4﹣2)÷2﹣[t﹣(﹣4)]×2÷2
=4×(4×2÷2),
解得t=4,
则P点坐标为(4,0).

练习册系列答案
相关题目