题目内容
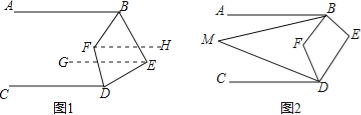
【题目】如图:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)

【答案】(1)140°;(2)6∠M+∠E=360°.(3)![]()
【解析】试题分析:(1)首先作EG∥AB,FH∥AB,利用平行线的性质可得∠ABE+∠CDE=280°,再利用角平分线的定义得到∠ABF+∠CDF=140°,从而得到∠BFD的度数;(2)先由已知得到∠ABE=6∠ABM,∠CDE=6∠CDM,由(1)得∠ABE+∠CDE=360°﹣∠E,∠M=∠ABM+∠CDM,等量代换,即可;
(3)由(2)的方法可得到2n∠M+∠E=360°,将∠E=m°代入可得![]() .
.
解:(1)作EG∥AB,FH∥AB,
∵AB∥CD,
∴EG∥AB∥FH∥CD,
∴∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,
∴∠ABE+∠BEG+∠GED+∠CDE=360°
∵∠BED=∠BEG+∠DEG=80°,
∴∠ABE+∠CDE=280°,
∵∠ABF和∠CDF的角平分线相交于E,
∴∠ABF+∠CDF=140°,
∴∠BFD=∠BFH+∠DFH=140°;
(2)∵∠ABM=∠ABF,∠CDM=∠CDF,
∴∠ABF=3∠ABM,∠CDF=3∠CDM,
∵∠ABE与∠CDE两个角的角平分线相交于点F,
∴∠ABE=6∠ABM,∠CDE=6∠CDM,
∴6∠ABM+6∠CDM+∠E=360°,
∵∠M=∠ABM+∠CDM,
∴6∠M+∠E=360°.
(3)由(2)结论可得,
2n∠ABN+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
解得:![]() .
.
故答案为:![]()

 阅读快车系列答案
阅读快车系列答案