题目内容
(2011•常德)已知△ABC,分别以AC和BC为直径作半圆O1,O2,P是AB的中点,
(1)如图1,若△ABC是等腰三角形,且AC=BC,在 ,
,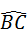 上分别取点E、F,使∠AO1E=∠BO2F
上分别取点E、F,使∠AO1E=∠BO2F ,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
(2)如图2,若(1)中△ABC是任意三角形,其他条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
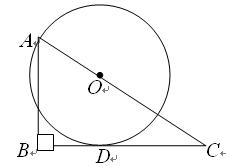
(3)如图3,若PC是⊙O1的切线,求证:AB2=BC2+3AC2.
(1)如图1,若△ABC是等腰三角形,且AC=BC,在
 ,
,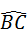 上分别取点E、F,使∠AO1E=∠BO2F
上分别取点E、F,使∠AO1E=∠BO2F ,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;(2)如图2,若(1)中△ABC是任意三角形,其他条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
(3)如图3,若PC是⊙O1的切线,求证:AB2=BC2+3AC2.

解:(1))∵P、O1、O2分别为AB、AC、BC的中点,
∴AP=BP,AO1=BO2,PO1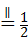 BC,PO2
BC,PO2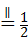 AC,
AC,
∴四边形PO1CO2是平行四边形,
∵AC=BC,∴PO1=PO2,
∴四边形PO1CO2是菱形;
(2)∵P、O1、O2分别为AB、AC、BC的中点,∴AP=BP,AO1=BO2,PO1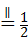 BC,PO2
BC,PO2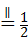 AC,
AC,
即PO1=BO2,AO1=PO2,
∴△APO1≌△BPO2;
(3)直角三角形APC中,设AP=c,AC=a,PC=b,
∴c2=a2+b2;AB2=4c2=4(a2+b2),
过点B作AC的垂线,交AC的延长线于D点.
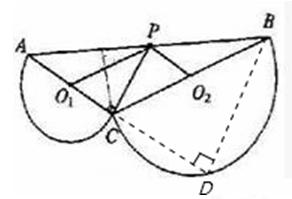
∴CD=a,BD=2b,BC2=a2+4b2,
∴BC2+3AC2=a2+4b2+3a2=4(a2+b2),
∴AB2=BC2+3AC2.
∴AP=BP,AO1=BO2,PO1
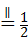 BC,PO2
BC,PO2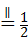 AC,
AC,∴四边形PO1CO2是平行四边形,
∵AC=BC,∴PO1=PO2,
∴四边形PO1CO2是菱形;
(2)∵P、O1、O2分别为AB、AC、BC的中点,∴AP=BP,AO1=BO2,PO1
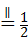 BC,PO2
BC,PO2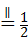 AC,
AC,即PO1=BO2,AO1=PO2,
∴△APO1≌△BPO2;
(3)直角三角形APC中,设AP=c,AC=a,PC=b,
∴c2=a2+b2;AB2=4c2=4(a2+b2),
过点B作AC的垂线,交AC的延长线于D点.

∴CD=a,BD=2b,BC2=a2+4b2,
∴BC2+3AC2=a2+4b2+3a2=4(a2+b2),
∴AB2=BC2+3AC2.
略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 ,
, ,则向量
,则向量 可表示为( ).
可表示为( ).




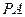 为
为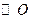 的切线,
的切线,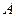 为切点,
为切点,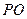 交
交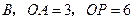 ,求
,求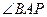 的度数.
的度数.
 中
中 ,
, 则⊙
则⊙
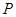 的正上方
的正上方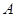 处,从
处,从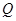 ,若∠
,若∠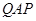 =
=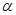 ,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( ) 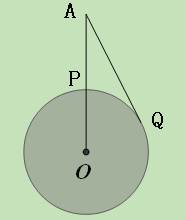
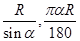
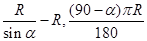
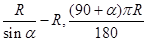
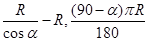
 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作

