Question

【题目】（2016浙江省衢州市）如图，正方形ABCD的顶点A，B在函数（x＞0）的图象上，点C，D分别在x轴，y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．

（1）当k=2时，正方形A′B′C′D′的边长等于____．

（2）当变化的正方形ABCD与（1）中的正方形A′B′C′D′有重叠部分时，k的取值范围是______________．

Answer 1

【答案】 ≤k≤18．

【解析】解：（1）如图，过点A′作AE⊥y轴于点E，过点B′⊥x轴于点F，则∠A′ED′=90°．

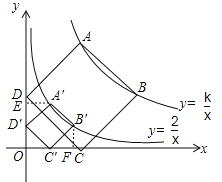
∵四边形A′B′C′D′为正方形，∴A′D′=D′C′，∠A′D′C′=90°，∴∠OD′C′+∠ED′A′=90°．∵∠OD′C′+∠OC′D′=90°，∴∠ED′A′=∠OC′D′．

在△A′ED′和△D′OC′中，∵∠ED′A′=∠OC′D′，∠A′ED′=∠D′OC′，A′D′=D′C′，∴△A′ED′≌△D′OC′（AAS），∴OD′=EA′，OC′=ED′．

同理△B′FC′≌△C′OD′．

设OD′=a，OC′=b，则EA′=FC′=OD′=a，ED′=FB′=OC′=b，即点A′（a，a+b），点B′（a+b，b）．∵点A′、B′在反比例函数的图象上，∴，解得：或（舍去）．

在Rt△C′OD′中，∠C′OD′=90°，OD′=OC′=1，∴C′D′==．

故答案为：．

（2）设直线A′B′解析式为，直线C′D′解析式为，∵点A′（1，2），点B′（2，1），点C′（1，0），点D′（0，1），∴有和，解得：和，∴直线A′B′解析式为y=﹣x+3，直线C′D′解析式为y=﹣x+1．设点A的坐标为（m，2m），点D坐标为（0，n）．

当A点在直线C′D′上时，有2m=﹣m+1，解得：m=，此时点A的坐标为（，），∴k=×=；

当点D在直线A′B′上时，有n=3，此时点A的坐标为（3，6），∴k=3×6=18．

综上可知：当变化的正方形ABCD与（1）中的正方形A′B′C′D′有重叠部分时，k的取值范围为≤k≤18．故答案为：≤k≤18．