题目内容
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.
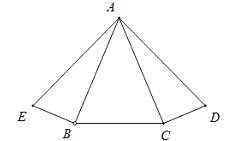
请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
【答案】AC,在同一个三角形中,等角对等边,AB,AE,HL,全等三角形对应角相等
【解析】
已知∠ABC=∠ACB,根据等腰三角形的判定方法可得AB=AC,在Rt△ABE和Rt△ACD中,利用HL证明Rt△ABE≌Rt△ACD,由全等三角形对应角相等即可得∠BAE=∠CAD.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= AC (在同一个三角形中,等角对等边)
在Rt△ABE和Rt△ACD中,
∵AB =AC, AE =AD,
∴Rt△ABE≌Rt△ACD(HL),
∴∠BAE=∠CAD(全等三角形对应角相等).

练习册系列答案
相关题目