题目内容
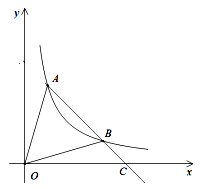
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
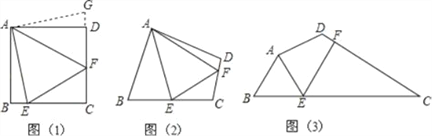
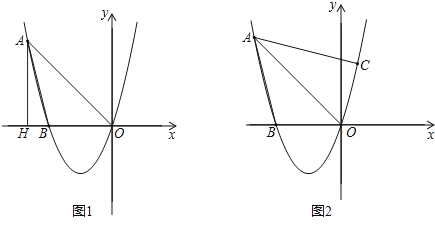
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)∠AOP=∠AOH+∠POH=45o+45o=90o;
(3)存在,直线AC解析式为![]()
【解析】试题分析:(1)根据已知点的坐标利用待定系数法确定二次函数的解析式即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,
试题解析:(1)由题意,得
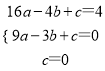 ,解得
,解得![]() .
.
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则![]()
解得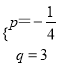 ,
,
∴直线AC解析式为y=![]() x+3
x+3

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案【题目】某校为了了解某个年级的学习情况,在这个年级抽取了50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组 | 50~59分 | 60~69分 | 70~79分 | 80~89分 | 90~99分 |
频率 | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
(1)本次测试90分以上的人数有________人;(包括90分)
(2)本次测试这50名学生成绩的及格率是________;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好 B.一般 C.不好