题目内容
如图①,梯形ABCD中,∠C=90°.动点E、F同时从点B出发,点E沿折线BA-AD-DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1cm/s.设E、F出发ts时,△EBF的面积为ycm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.请根据图中的信息,解答下列问题:(1)梯形上底的长AD=
(2)当点E在BA、DC上运动时,分别求出y与t的函数关系式(注明自变量的取值范围);
(3)当t为何值时,△EBF与梯形ABCD的面积之比为1:2?
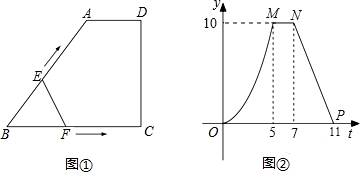
分析:(1)此题的关键是要理解分段函数的意义,OM段是曲线,说明E、F分别在BA、BC上运动,此时y、t的关系式是二次函数;MN段是线段,且平行于t轴,那么此时F运动到终点C,且E在线段AD上运动,此时y为定值;NP段是线段,此时y、t的函数关系式是一次函数,此时E在线段CD上运动,此时y值随t的增大而减小;
根据上面的分析,可知在MN之间时,E在线段AD上运动,在这个区间E点运动了2秒,所以AD=2cm;
根据OM段的函数图象知:当t=5时,E、F分别运动到A、C两点,那么AB=BC=5;根据MN段函数图象知:此时△BEF的面积为10,可据此求出梯形的高为4,进而可根据梯形的面积公式求出梯形ABCD的面积;
(2)利用待定系数法分别求两个解析式;
(3)当E在AD上运动时,△EBF的面积为10,显然不符合题意,所以当△EBF与梯形ABCD的面积之比为1:2时,E点一定在线段BA或线段CD上,可将△EBF的面积(即梯形面积的一半)代入(2)题求得的两个函数关系式中,即可得到所求的t值.
根据上面的分析,可知在MN之间时,E在线段AD上运动,在这个区间E点运动了2秒,所以AD=2cm;
根据OM段的函数图象知:当t=5时,E、F分别运动到A、C两点,那么AB=BC=5;根据MN段函数图象知:此时△BEF的面积为10,可据此求出梯形的高为4,进而可根据梯形的面积公式求出梯形ABCD的面积;
(2)利用待定系数法分别求两个解析式;
(3)当E在AD上运动时,△EBF的面积为10,显然不符合题意,所以当△EBF与梯形ABCD的面积之比为1:2时,E点一定在线段BA或线段CD上,可将△EBF的面积(即梯形面积的一半)代入(2)题求得的两个函数关系式中,即可得到所求的t值.
解答:解:(1)由图可知:OM段为抛物线,此时点E、F分别在BA、BC上运动;
当E、A重合,F、C重合时,t=5s,
∴AB=BC=5cm;
MN段是线段,且平行于t轴,此时F运动到终点C,E点在线段AD上运动;
∴AD=1×2=2cm,CD=2×S△BEF÷BC=2×10÷5=4cm;
∴S梯形ABCD=
(AD+BC)•CD=
×(2+5)×4=14cm2;
故填:2,14;
(2)当点E在BA上运动时,设抛物线的解析式为y=at2,把M点的坐标(5,10)代入得a=
,
∴y=
t2,0≤t≤5;
当点E在DC上运动时,设直线的解析式为y=kt+b,
把P(11,0),N(7,10)代入,得11k+b=0,7k+b=10,解得k=-
,b=
,
所以y=-
t+
,(7<t≤11)
(3)当0<t≤5时,
t2=
×14,
∴t=
;
当7<t≤11时,-
t+
=
×14,
∴t=8.2;
∴t=
s或8.2s时,△BEF与梯形ABCD的面积比为1:2.
当E、A重合,F、C重合时,t=5s,
∴AB=BC=5cm;
MN段是线段,且平行于t轴,此时F运动到终点C,E点在线段AD上运动;
∴AD=1×2=2cm,CD=2×S△BEF÷BC=2×10÷5=4cm;
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
故填:2,14;
(2)当点E在BA上运动时,设抛物线的解析式为y=at2,把M点的坐标(5,10)代入得a=
| 2 |
| 5 |
∴y=
| 2 |
| 5 |
当点E在DC上运动时,设直线的解析式为y=kt+b,
把P(11,0),N(7,10)代入,得11k+b=0,7k+b=10,解得k=-
| 5 |
| 2 |
| 55 |
| 2 |
所以y=-
| 5 |
| 2 |
| 55 |
| 2 |
(3)当0<t≤5时,
| 2 |
| 5 |
| 1 |
| 2 |
∴t=
| ||
| 2 |
当7<t≤11时,-
| 5 |
| 2 |
| 55 |
| 2 |
| 1 |
| 2 |
∴t=8.2;
∴t=
| ||
| 2 |
点评:此题主要考查了分段函数的应用、梯形的性质以及图形面积的求法;能够正确的理解分段函数的意义是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数. 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=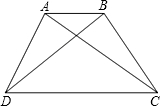 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=