题目内容
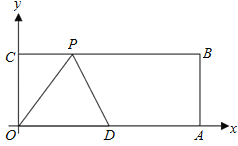
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当ΔODP是腰长为5的等腰三角形时，点P的坐标为___________
【答案】（1，3）或（4，3）或（9，3）．
【解析】试题分析：根据当OP=OD时，以及当OD=PD时，分别进行讨论得出P点的坐标．
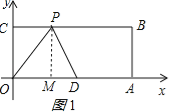
解：过P作PM⊥OA于M
（1）当OP=OD时，如图1所示：
OP=5，CO=3，
由勾股定理得：CP=4，
∴P（4，3）；
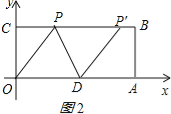
（2）当OD=PD时如图2所示：
PD=DO=5，PM=3，
由勾股定理得：MD=4，
∴CP=5﹣4=1或CP'=9，
∴P（1，4）或（9，3）；
综上，满足题意的点P的坐标为（1，3）、（4，3）、（9，3），
故答案为：（1，3）或（4，3）或（9，3）．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
