题目内容
【题目】直线l1:y=﹣2x+5与y轴交于点B,直线l2:y=kx+b与x轴交于点D(1,0),与y轴交于点C,两直线交于点A(2,1).
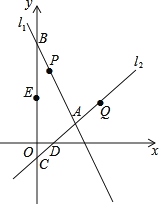
(1)求直线l2的函数解析式.
(2)求两直线与y轴围成的三角形的面积.
(3)点P为l1上一动点,点Q为l2上一动点,点E(0,2),若以BE为一边,且以点B,E,P,Q为顶点的四边形为平行四边形,直接写出点Q的坐标.
【答案】(1)y=x﹣1;(2)两直线与y轴围成的三角形的面积为6;(3)Q(1,0)或(3,2).
【解析】
(1)根据待定系数法即可求得;
(2)根据函数解析式求得B、C的坐标,然后根据三角形面积公式求得即可;
(3)根据图象可知要使以点B,E,P,Q为顶点的四边形为平行四边形,则PQ∥BE且PQ=BE,故可设P(m,-2m+5),则Q(m,m-1),列出关于m的方程,解方程即可求得m的值,从而求得Q的坐标.
(1)∵直线l2:y=kx+b与x轴交于点D(1,0),与直线l1:y=-2x+5交于点A(2,1).
∴![]() ,解得
,解得![]() ,
,
∴直线l2的函数解析式为y=x-1;
(2)∵直线l1:y=-2x+5与y轴交于点B,
∴B(0,5),
∵直线l2:y=x-1与y轴交于点C,
∴C(0,-1),
∴BC=5+1=6,
∴S△ABC=![]() ×6×2=6;
×6×2=6;
∴两直线与y轴围成的三角形的面积为6;
(3)要使以点B,E,P,Q为顶点的四边形为平行四边形,则PQ∥BE且PQ=BE,
设P(m,-2m+5),则Q(m,m-1),
∵BE=5-2=3,
∴|-2m+5-(m-1)|=3,
解得m=1或m=3,
∴Q(1,0)或(3,2).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目