题目内容
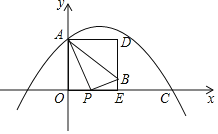
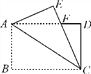
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于_________.
【答案】![]()
【解析】分析:根据折叠的性质得到AE=AB,∠E=∠B=90°,易证Rt△AEF≌Rt△CDF,即可得到结论EF=DF;易得FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中利用勾股定理得到关于x的方程x2=42+(6﹣x)2,解方程求出x,即可得到结论.
详解:∵矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,∴AE=AB,∠E=∠B=90°.
又∵四边形ABCD为矩形,∴AB=CD,∴AE=DC,而∠AFE=∠DFC.
在△AEF与△CDF中,∵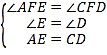 ,∴△AEF≌△CDF(AAS),∴EF=DF;
,∴△AEF≌△CDF(AAS),∴EF=DF;
∵四边形ABCD为矩形,∴AD=BC=6,CD=AB=4.
∵Rt△AEF≌Rt△CDF,∴FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中,CF2=CD2+DF2,即x2=42+(6﹣x)2,解得:x=![]() ,则FD=6﹣x=
,则FD=6﹣x=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】抛物线y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,﹣2);
③抛物线的对称轴是:x=1;
④在对称轴左侧,y随x增大而增大.
A. 1 B. 2 C. 3 D. 4