题目内容
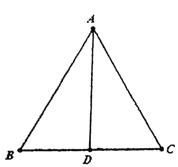
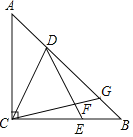
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据题意和图形,利用全等三角形的判定可以证明结论成立;
(2)根据题意和(1)中的结论,利用全等三角形的性质和等腰三角形的判定可以证明结论成立.
证明:(1)∵∠CDB=∠DEC,
∴∠ADC=∠BED,
∵AC=BC,
∴∠A=∠B,
在△ACD与△BDE中,
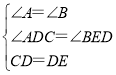 ,
,
∴△ACD≌△BDE(AAS);
(2)由(1)知,△ACD≌△BDE,
∴∠ACD=∠BDE,
∵在Rt△ACB中,AC=BC,
∴∠A=∠B=45°,
∴∠CDG=45°+∠ACD,∠DGC=45°+∠BCG,
∴∠CDF=45°,
∵CF⊥DE交BD于点G,
∴∠DFC=90°,
∴∠DCF=45°,
∵DC=DE,
∴∠DCE=∠DEC,
∵∠DCE=∠DCF+∠BCG=45°+∠BCG,∠DEC=∠B+∠BDE=45°+∠BDE,
∴∠BCG=∠BDE,
∴∠ACD=∠BCG,
∴∠CDG=∠CGD,
∴CD=CG,
∴△CDG是等腰三角形.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目