题目内容
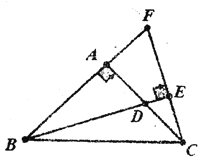
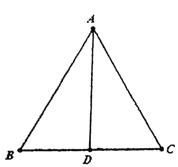
【题目】如图,在△ABC中,AB=AC,D是BC的中点,则下列结论正确的是( )
①△ABD≌△ACD;②∠B=∠C;③∠BAD=∠CAD;④AD⊥BC
A. ①②③B. ②③④C. ①②④D. ①②③④
【答案】D
【解析】
利用SSS证明△ABD≌△ACD,根据全等三角形的性质可得∠B=∠C、∠BAD=∠CAD、∠BDA=∠CDA,再由∠BDA+∠CDA=180°,即可得∠BDA=∠CDA=90°,所以AD⊥BC.
∵D是BC的中点,
∴BD=CD,
在△ABD与△ACD中,
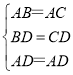 ,
,
∴△ABD≌△ACD;
∴∠B=∠C,∠BAD=∠CAD,∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC.
综上,正确的结论为①②③④.
故选D.

练习册系列答案
相关题目