题目内容
【题目】已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,![]() ),且∠BDC=90°,求点C的坐标;
),且∠BDC=90°,求点C的坐标;
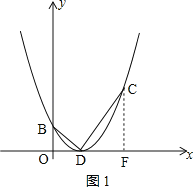
(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.

【答案】(1)y=![]() (x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
(x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
【解析】(1)将点(3,1)代入解析式求得a的值即可;
(2)设点C的坐标为(x0,y0),其中y0=![]() (x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得
(x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() 据此求得x0的值即可得;
据此求得x0的值即可得;
(3)①设点P的坐标为(x1,y1),点Q为(x2,y2),联立直线和抛物线解析式,化为关于x的方程可得![]() ,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=
,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=![]() (x1﹣1)2、QN=y2=
(x1﹣1)2、QN=y2=![]() (x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即
(x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即![]() =
=![]() ,从而得△PMD∽△DNQ,据此进一步求解可得;
,从而得△PMD∽△DNQ,据此进一步求解可得;
②过点D作x轴的垂线交直线PQ于点G,则DG=4,根据S△PDQ=![]() DGMN列出关于k的等式求解可得.
DGMN列出关于k的等式求解可得.
(1)将点(3,1)代入解析式,得:4a=1,
解得:a=![]() ,
,
所以抛物线解析式为y=![]() (x﹣1)2;
(x﹣1)2;
(2)由(1)知点D坐标为(1,0),
设点C的坐标为(x0,y0),(x0>1、y0>0),
则y0=![]() (x0﹣1)2,
(x0﹣1)2,
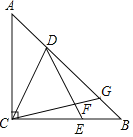
如图1,过点C作CF⊥x轴,
∴∠BOD=∠DFC=90°、∠DCF+∠CDF=90°,
∵∠BDC=90°,
∴∠BDO+∠CDF=90°,
∴∠BDO=∠DCF,
∴△BDO∽△DCF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
解得:x0=17,此时y0=64,
∴点C的坐标为(17,64).
(3)①证明:设点P的坐标为(x1,y1),点Q为(x2,y2),(其中x1<1<x2,y1>0,y2>0),
由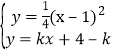 ,得:x2﹣(4k+2)x+4k﹣15=0,
,得:x2﹣(4k+2)x+4k﹣15=0,
∴![]() ,
,
∴(x1﹣1)(x2﹣1)=﹣16,
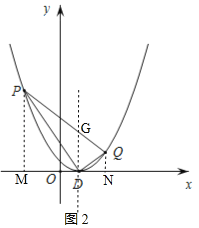
如图2,分别过点P、Q作x轴的垂线,垂足分别为M、N,
则PM=y1=![]() (x1﹣1)2,QN=y2=
(x1﹣1)2,QN=y2=![]() (x2﹣1)2,
(x2﹣1)2,
DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1,
∴PMQN=DMDN=16,
∴![]() =
=![]() ,
,
又∠PMD=∠DNQ=90°,
∴△PMD∽△DNQ,
∴∠MPD=∠NDQ,
而∠MPD+∠MDP=90°,
∴∠MDP+∠NDQ=90°,即∠PDQ=90°;
②过点D作x轴的垂线交直线PQ于点G,则点G的坐标为(1,4),
所以DG=4,
∴S△PDQ=![]() DGMN=
DGMN=![]() ×4×|x1﹣x2|=2
×4×|x1﹣x2|=2![]() =8
=8![]() ,
,
∴当k=0时,S△PDQ取得最小值16.