Question

如图，P是反比例函数图象在第二象限上的一点，且长方形PEOF的面积为8，则反比例函数的表达式是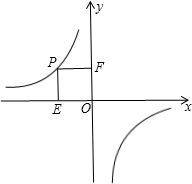

 

．

Answer 1

分析：因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的矩形的面积S是个定值，即S=|k|，再结合反比例函数所在的象限即可得到k的值，则反比例函数的解析式即可求出．

解答：解：设反比例函数的表达式是 y=

k

x

（k≠0），
由题意知，S_矩形PEOF=|k|=8，
所以k=±8，
又反比例函数图象在第二象限上，k＜0，
所以k=-8，
即反比例函数的表达式是y=-

8

x

．
故答案为：y=-

8

x

．

点评：本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．本知识点是中考的重要考点，同学们应高度关注．