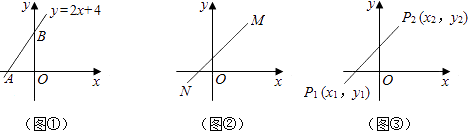题目内容
【题目】定义：如图1，抛物线
与
轴交于A，B两点，点P在抛物线上（点P与A，B两点不重合），如果△ABP的三边满足
，则称点P为抛物线的勾股点。
（1）直接写出抛物线
的勾股点的坐标；
（2）如图2，已知抛物线C：
与
轴交于A，B两点，点P（1，
）是抛物线C的勾股点，求抛物线C的函数表达式；
（3）在（2）的条件下，点Q在抛物线C上，求满足条件
的点Q（异于点P）的坐标
【答案】（1）（0，1）；（2）y=﹣
x2+
x；（3）（3，
）或（2+
，﹣）或（2﹣，﹣）．
【解析】
试题分析：（1）根据抛物线勾股点的定义即可求解；
（2）作PG⊥x轴，由P点坐标求得AG=1、PG=、 PA=2，由tan∠PAB=
知∠PAG=60°,从而求得AB=4，即B（4，0），运用待定系数法即可求解；
（3）由SΔABQ=SΔABP且两三角形同底，可知点Q到x轴的距离为
，据此可求解.
试题解析： （1）抛物线y=﹣x2+1的勾股点的坐标为（0，1）；
（2）抛物线y=ax2+bx过原点，即点A（0，0），
如图，作PG⊥x轴于点G，
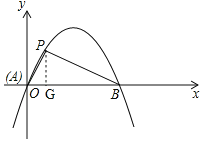
∵点P的坐标为（1，），
∴AG=1、PG=，PA=
=2，
∵tan∠PAB=，
∴∠PAG=60°，
在Rt△PAB中，AB=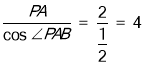
，
∴点B坐标为（4，0），
设y=ax（x﹣4），
将点P（1，）代入得：a=﹣，
∴y=﹣x（x﹣4）=﹣x2+x；
（3）①当点Q在x轴上方时，由S△ABQ=S△ABP知点Q的纵坐标为，
则有﹣x2+x =，
解得：x1=3，x2=1（不符合题意，舍去），
∴点Q的坐标为（3，）；
②当点Q在x轴下方时，由S△ABQ=S△ABP知点Q的纵坐标为﹣
则有﹣x2+x =﹣，
解得：x1=2+，x2=2﹣，
∴点Q的坐标为（2+，﹣）或（2﹣，﹣）；
综上，满足条件的点Q有3个：（3，）或（2+，﹣）或（2﹣，﹣）．
