题目内容
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.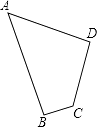
(1)判断∠D是否是直角,并说明理由.
(2)求四边形草坪ABCD的面积.
【答案】
(1)解:∠D是直角,理由如下:
连接AC,
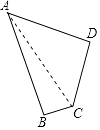
∵∠B=90°,AB=24m,BC=7m,
∴AC2=AB2+BC2=242+72=625,
∴AC=25(m).
又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,
∴△ACD是直角三角形,或∠D是直角
(2)解:S四边形ABCD=S△ABC+S△ADC
= ![]() ABBC+
ABBC+ ![]() ADDC
ADDC
=234(m2).
【解析】(1)连接AC,先根据勾股定理求出AC的长,再依据勾股定理的逆定理得到∠D是直角;
(2)由题意可知S四边形ABCD=S△ABC+S△ADC,然后将四边形ABCD的面积转化为两个直角三角形的面积之和求解即可.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目