题目内容
【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程
，操作步骤是：
第一步：根据方程的系数特征，确定一对固定点A（0，1），B（5，2）；
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C的横坐标m即为该方程的一个实数根（如图1）；
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D的横坐标n即为该方程的另一个实数根．
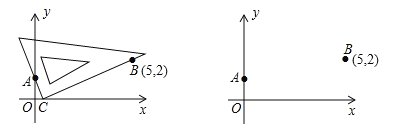
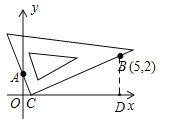
（1）在图2中，按照“第四步”的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）；
（2）结合图1，请证明“第三步”操作得到的m就是方程的一个实数根；
（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程
（a≠0，
≥0）的实数根，请你直接写出一对固定点的坐标；
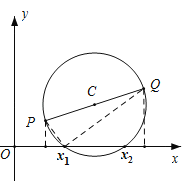
（4）实际上，（3）中的固定点有无数对，一般地，当m1，n1，m2，n2与a，b，c之间满足怎样的关系时，点P（m1，n1），Q（m2，n2）就是符合要求的一对固定点？
【答案】（1）作图见解析；（2）证明见解析；（3）A（0，1），B（﹣
，
）或A（0，
），B（﹣，c）等；（4）
，
=．
【解析】
试题分析：（1）根据“第四步”的操作方法作出点D即可；
（2）过点B作BD⊥x轴于点D，根据△AOC∽△CDB，可得
，进而得出
，即
，据此可得m是方程
的实数根；
（3）方程
（a≠0）可化为
，模仿研究小组作法可得一对固定点的坐标；
（4）先设方程的根为x，根据三角形相似可得
，进而得到
，再根据，可得，最后比较系数可得m1，n1，m2，n2与a，b，c之间的关系．
试题解析：（1）如图所示，点D即为所求；
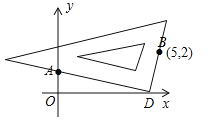
（2）如图所示，过点B作BD⊥x轴于点D，根据∠AOC=∠CDB=90°，∠ACO=∠CBD，可得△AOC∽△CDB，∴，∴，∴m（5﹣m）=2，∴，∴m是方程的实数根；
（3）方程（a≠0）可化为 ，模仿研究小组作法可得：A（0，1），B（﹣，）或A（0，），B（﹣，c）等；
（4）如图，P（m1，n1），Q（m2，n2），设方程的根为x，根据三角形相似可得，上式可化为，又∵，即，∴比较系数可得，=．
