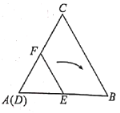题目内容
【题目】如图,在![]() 中,高
中,高![]() 相交于点
相交于点![]() ,图中与
,图中与![]() 相似的三角形共有( )
相似的三角形共有( )
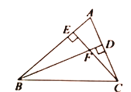
A.1个B.2个C.3个D.4个
【答案】C
【解析】
先利用高的定义得到∠BEC=∠BDC=90°,再利用等角的余角相等得到∠ABD=∠ACE,加上∠A=∠A,根据有两组角对应相等的两个三角形相似可判断△ABD∽△ACE,利用同样的方法得到△FBE∽△ABD,△FCD∽△ACE,所以△FBE∽△ABD∽△ACE∽△FCD.
解:∵高BD、CE相交于点F,
∴∠BEC=∠BDC=90°,
∵∠BFE=∠CFD,
∴∠ABD=∠ACE,
∵∠A=∠A,
∴△ABD∽△ACE,
∵∠ABD=∠FBE,∠BEF=∠BDA,
∴△FBE∽△ABD,
同理可得△FCD∽△ACE,
∴△FBE∽△ABD∽△ACE∽△FCD.
故选C.

练习册系列答案
相关题目