题目内容
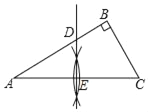
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.

【答案】(1)作图见解析(2)10+![]() .
.
【解析】分析:(1)垂直平分线的尺规作图方法:先以A为圆心,以大于线段AC一半的长度画弧,然后再以C为圆心,以相同长度为半径画弧,两条圆弧交于两点,连接该两点的直线即为线段AC的垂直平分线。(2)先化简,然后利用三角形的周长求出a,最后代入即可求得T的值。
详解:(1)如图所示,DE即为所求;
(2)由题可得,AE=![]() AC=
AC=![]() ,∠A=30°,
,∠A=30°,
∴Rt△ADE中,DE=![]() AD,
AD,
设DE=x,则AD=2x,
∴Rt△ADE中,x2+(![]() )2=(2x)2,
)2=(2x)2,
解得x=1,
∴△ADE的周长a=1+2+![]() =3+
=3+![]() ,
,
∵T=(a+1)2﹣a(a﹣1)=3a+1,
∴当a=3+![]() 时,T=3(3+
时,T=3(3+![]() )+1=10+3
)+1=10+3![]() .
.

【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?