题目内容
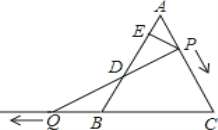
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

【答案】(1)![]() x;(2)x=4;(3)
x;(2)x=4;(3)![]() 或
或![]() ;(4)3,6,
;(4)3,6,  .
.
【解析】试题分析:(1)利用平行四边形和三角函数值,可求出PE长.(2)利用三角函数把AP,PC用x表示出来,求值.(3)AP的长度分类讨论,可求得两个二次函数解析式.(4)求E到各边的距离,直接写出结果.
试题解析:
(1)∠C=90°,AB=AC,∴∠A=45°,
∵PD![]() AB,∴AD=APcos∠A=
AB,∴AD=APcos∠A=![]() x=PD,
x=PD,
∵四边形PADE是平行四边形,
PE=AD=![]() x.
x.
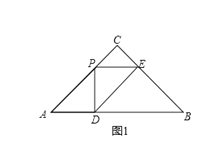
(2)当E点落在BC上,图1,PE![]() AD,∴∠CPE=45°,
AD,∴∠CPE=45°,
∴PC=PEcos∠CPE=![]() x
x![]() =
=![]() ,
,
所以AP+PC=AC,
所以x+![]() =6, x=4.
=6, x=4.
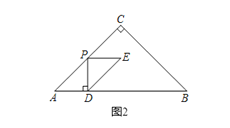
(3)当0<x![]() 时,y=AD
时,y=AD![]() .图2,
.图2,
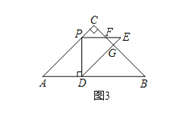
当4<x![]() 6,设DE与 BC交于G,PE与BC交于F,图3,
6,设DE与 BC交于G,PE与BC交于F,图3,
AD=![]() x,AB=
x,AB=![]() AC=6
AC=6![]() ,
,
∴DB=AB![]() AD=6
AD=6![]() -
-![]() x,
x,
∴DG=DBsin∠B=6-![]() ,
,
∴GE=DE-DG=![]() ,
,
y=S四边形PADE-S△GFE=![]() 2
2
= ![]() .
.
(4)3,6, 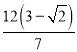 .
.

练习册系列答案
相关题目