��Ŀ����
����Ŀ������ƽ���ڸ�������OA������OB����MON���������¶��壺��������OA��OB��ɵġ�AOB��ƽ����OT���ڡ�MON���ڲ����OM��ON�ϣ��������OA������OB���ڡ�MON�ں��Գ�.���磬ͼ1������OA������OB���ڡ�MON�ں��Գ�

��֪����ͼ2����ƽ���ڣ���AOM=10������MON=20��
��1��������������![]() ��
��![]() ��λ����ͼ3��ʾ����
��λ����ͼ3��ʾ����![]() ��
��![]() �����������������У�������OA���ڡ�MON�ں��ԳƵ�������_____________
�����������������У�������OA���ڡ�MON�ں��ԳƵ�������_____________
��2������OC��ƽ�����Ƶ�O��ת��һ�������ߣ�������OA������OC���ڡ�MON�ں��Գƣ����COM=x������x��ȡֵ��Χ��
��3����ͼ4����AOE=��EOH=2��FOH=20�����ֽ�����OH�Ƶ�O��ÿ��1�����ٶ�˳ʱ����ת��ͬʱ������OE��OF�Ƶ�O����ÿ��3�����ٶ�˳ʱ����ת.����ת��ʱ��Ϊt�룬��![]() .����FOE���ڲ����������ٴ���һ����OΪ���������������OH���ڡ�MON�ں��Գƣ�ֱ��д��t��ȡֵ��Χ.
.����FOE���ڲ����������ٴ���һ����OΪ���������������OH���ڡ�MON�ں��Գƣ�ֱ��д��t��ȡֵ��Χ.

���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
��1���������⣬�����AOB2�������ж����ƽ�������ڡ�MON���ڲ���
��2������������OA������OC���ڡ�MON�ں��Գƣ����Ƴ���AOC��ȡֵ��Χ��Ȼ�ɵó���COM��ȡֵ��Χ��
��3�����ȸ�������ó����ƽ���ߵ���ת�ٶȣ�����ֱ���ת��OM��ON����ʱ�����ɵý�.
��1���ߡ�AOM=10������MON=20����![]() ��
��![]()
���AOB2=��AOM+��B2OM=10��+15��=25��
�����ƽ�������ڡ�MON���ڲ�
��������OA���ڡ�MON�ں��ԳƵ�������![]() ��
��
��2��������OA������OC���ڡ�MON�ں��Գƣ���
![]()
��![]()
�ߡ�COM=x������COM=��AOC-��AOM
��![]()
(3)�������⣬�ɵ����ƽ���ߵ���ת�ٶ���ÿ��2������
������ת��OM��ON����ʱ����FOE���ڲ����������ٴ���һ����OΪ���������������OH���ڡ�MON�ں��Գƣ���
������ת��OM����ʱ����ͼ��ʾ��
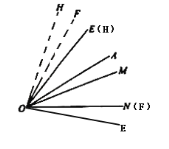
OE��OF��ת��60�㣬OH��ת��20�㣬��![]() ��
��
������ת��ON����ʱ����ͼ��ʾ��
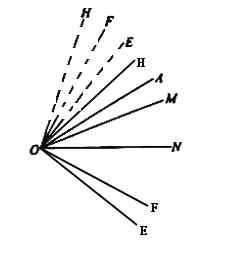
OE��OF��ת��90�㣬OH��ת��30�㣬��![]()
��![]()
�ʴ�Ϊ![]() .
.

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�