Question

【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义：若y′= ,则称点Q为点P的“可控变点”。例如：点(1,2)的“可控变点”为点(1,2).

结合定义，请回答下列问题：

(1)点(3,4)的“可控变点”为点 ___.

(2)若点N(m,2)是函数y=x1图象上点M的“可控变点”，则点M的坐标为___；

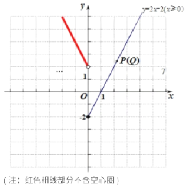
(3)点P为直线y=2x2上的动点,当x0时,它的“可控变点”Q所形成的图象如图所示(实线部分含实心点).请补全当x<0时，点P的“可控变点”Q所形成的图象.

Answer 1

【答案】（1）(3,4)；（2）（2）(3,2)或(1,2)；（3）见解析；

【解析】

（1）根据“可控变点”的定义可得点（-3，4）的“可控变点”的坐标；

（2）分两种情况进行讨论：当m≥0时，点M的纵坐标为2，令2=x-1，则x=3，即M（3，2）；当m<0时，点M的纵坐标为-2，令-2=x-1，则x=3，即M（-1，-2）；

（3）根据P（x，2x-2），当x<0时，点P的“可控变点”Q为（x，-2x+2），可得Q的纵坐标为-2x+2，即Q的坐标符合函数解析式y=-2x+2，据此可得当x<0时，点P的“可控变点”Q所形成的图象．

(1)根据“可控变点”的定义可得,点(3,4)的“可控变点”为点(3,4)；

故答案为：(3,4)；

(2)∵点N(m,2)是函数y=x1图象上点M的“可控变点”，

∴①当m0时,点M的纵坐标为2,令2=x1,则x=3,即M(3,2)；

②当m<0时,点M的纵坐标为2,令2=x1,则x=3,即M(1,2)；

∴点M的坐标为(3,2)或(1,2)；

故答案为：(3,2)或(1,2)；

(3)∵点P为直线y=2x2上的动点，

∴P(x,2x2)，

当x<0时,点P的“可控变点”Q为(x,2x+2)，

即Q的纵坐标为2x+2，即Q的坐标符合函数解析式y=2x+2，

∴当x<0时，点P的“可控变点”Q所形成的图象如下图；