题目内容
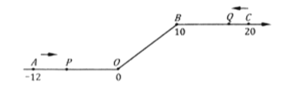
【题目】如图,点A,B在数轴上表示的数分别为-2与+6,动点P从点A出发,沿A→B以每秒2个单位长度的速度向终点B运动,同时,动点Q从点B出发,沿B→A以每秒4个单位长度的速度向终点A运动,当一个点到达时,另一点也随之停止运动.

(1)当Q为AB的中点时,求线段PQ的长;
(2)当Q为PB的中点时,求点P表示的数.
【答案】(1)2;(2)![]()
【解析】
(1)根据两点间的距离公式得出AB=8,根据线段中点的定义得出QB=4,根据路程除以速度等于时间得出当点Q为AB中点的时候,运动时间是1秒,此时AP=2,由PQ= AB-AP-BQ 即可算出答案;
(2) 设点P,Q的运动时间为t秒,则AP=2t,BQ=4t , PQ=AB-AP-BQ=8-6t ,根据线段中点的定义得出 PQ=BQ ,从而列出方程,求解即可.
(1)解:∵Q为AB的中点,AB=8,
OB=![]() AB=4.
AB=4.
∵点Q的运动速度为每秒4个单位长度,
∴点Q的运动时间为1秒.
∵点P的运动速度为每秒2个单位长度,
∴点P的运动路程为2个单位长度,即AP=2.
∴PQ=AB-AP-BQ=2
(2)解:设点P,Q的运动时间为t秒,则AP=2t,BQ=4t,
∴PQ=AB-AP-BQ=8-6t,
∵Q为PB的中点,
∴PQ=BQ,即8-6t=4t,
∴t=![]() ,∴AP=
,∴AP=![]() ,
,
∵![]() -2=
-2=![]() ,
,
∴点P表示的有理数是![]() .
.

练习册系列答案
相关题目