题目内容
【题目】某商场准备购进A、B两种商品进行销售,若A种商品的进价比B种商品的进价每件少 5元,且用 90元购进A种商品的数量比用100元购进B种商品的数量多1件.
(1)求A、B两种商品的进价每件分别是多少元?
(2)若该商场购进A种商品的数量是B种商品数量的3倍少4 件,两种商品的总件数不超过96件;A种商品的销售价格为每件30元,B种商品的销售价格为每件38元,两种商品全部售出后,可使总利润超过1200元.该商场购进A、B两种商品有哪几种方案?
【答案】(1)A:15,B:20;(2)详见解析.
【解析】分析:(1)关键语是“用 90元购进A种商品的数量比用100元购进B种商品的数量多1件”可根据此列出方程;
(2)本题中“根据进两种零件的总数量不超过96个”可得出关于数量的不等式方程,根据“使销售两种零件的总利润(利润=售价-进价)超过1200元”可得出关于利润的不等式方程,组成方程组后得出未知数的取值范围,然后根据取值的不同情况,列出不同的方案.
解:(1)设B种商品的进价为每件x元,则A种商品的进价为每件(x-5)元.
由题意得![]()
解得x1=20,x2=-25
经检验:x2=-25是原分式方程的解,但不符合实际意义,故舍去;
x1=20是原分式方程的解,且符合实际意义.
∴x=20, x-5=15(元).
答:A种商品的进价为每件15元,B种商品的进价为每件20元.
(2) 设购进B种商品y件,则购进A种商品(3y-4)件.
由题意得![]()
解得 20<y≤25
∵y为整数,∴y=21或22或23或24或25,
∴当y=21时,3y-4=59;y=22时,3y-4=62;y=23时,3y-4=65;y=24时,3y-4=68;
y=25时,3y-4=71;
所以该商场购进A、B两种商品有5种方案:方案一:购进A种商品59件,B种商品21件;方案二:购进A种商品62件,B种商品22件;方案三:购进A种商品65件,B种商品23件;方案四:购进A种商品68件,B种商品24件;方案五:购进A种商品71件,B种商品25件

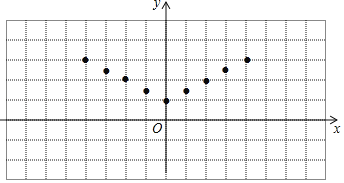
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .