题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,AD平分
,AD平分![]() 交OB于D,
交OB于D,![]() 交AB于E,垂足为F.
交AB于E,垂足为F.
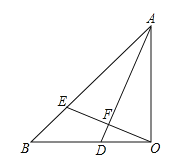
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)AD-OE= 2.
【解析】
(1)由题意可证△EAF≌△OAF,连接DE,可证AD为EO的垂直平分线,则ED=DO,又可证△BED为等腰直角三角形,则可证得BE=OD;
(2)在AD上截AM=OE,可证得△AMO≌△OEB,可得OD=OM,又因为AD⊥EO,则可得MF=FD,则可得AD-OE=2DF=2.
(1)证明:连接DE,
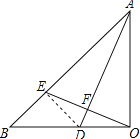
∵OE⊥AD,
∴∠AFE=∠AFO=90°,
∵AD平分∠EAO,
∴∠EAF=∠OAF,
在△EAF和△OAF中
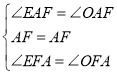 ,
,
∴△EAF≌△OAF(ASA),
∴AE=AO,∠AEO=∠AOE,
∵AD⊥OE,
∴EF=FO,
∴DE=DO,
∴∠DEO=∠DOE,
∵∠AEO=∠AOE,
∴∠AED=∠AOB=90°,
∵∠AOB=90°,AO=BO,
∴∠B=45°,
∴∠EDB=∠AEO-∠B=90°-45°=45°=∠B,
∴BE=DE,
∴OD=BE;
(2)解:在AD上截AM=OE,连接OM,
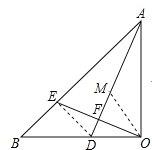
∵∠OAB=∠B=45°,AD平分∠OAB,
∴∠OAM=22.5°,
∵OD=DE,
∴∠DEO=∠DOE,
∵∠EDB=45°=∠DEO+∠DOE,
∴∠EOB=22.5°=∠OAM,
在△AMO和△OEB中,
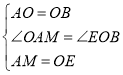 ,
,
∴△AMO≌△OEB(SAS),
∴MO=BE=OD,
∵OE⊥AD,
∴DF=MF,
∴AD-OE=DM=2DF=2.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
【题目】如图1是2019年11月的日历,用如图2所示的曲尺形框框(有三个方向,从左往右依次记为一、二、三个框) ,可以框住日历中的三个数,设被框住的三个数中最大的数为![]()
日 | 一 | 二 | 三 | 四 | 五 | 六 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

![]() 请用含
请用含![]() 的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
![]() 这三个框分别框住的中间的数之和能恰好是
这三个框分别框住的中间的数之和能恰好是![]() 的倍数吗?如能请求出
的倍数吗?如能请求出![]() 的值,若不能请说明理由.
的值,若不能请说明理由.