Question

【题目】如图，将正方形ABCD的一角折向边CD，使点A与CB上一点E重合，若BE=1，CE=2，则折痕FG的长度为（ ）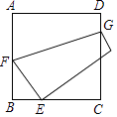
A.
B.2
C.3
D.4

Answer 1

【答案】A
【解析】解：过G作GM⊥AB于M，连接AE，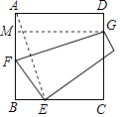
则MG=AD=AB，
∵将正方形ABCD的一角折向边CD，使点A与CB上一点E重合，
∴AE⊥GF，
∴∠FAE+∠AFG=∠AFG+∠MGF，
∴∠BAE=∠MGF，
在△ABE与△MGF中 ，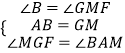
∴△ABE≌△GMF，
∴MF=BE=1，
∵MG=AD=BC=3，
∴FG= = ，
故选A．
【考点精析】根据题目的已知条件，利用正方形的性质和翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．