题目内容
【题目】△ABC的顶点均在边长为1的小正方形网络中的格点上,如图,建立平面直角坐标系,点B在x轴上.
(1)在图中画出△ABC关于x轴对称的△A’B’C’,连接AA’,求证:△AA’C≌△A’AC’;
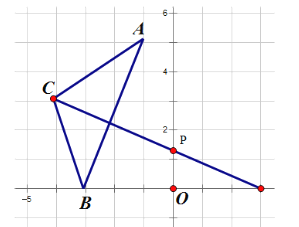
(2)请在y轴上画点P,使得PB+PC最短.(保留作图痕迹,不写画法)

【答案】(1)作图见解析;(2)作图见解析.
【解析】试题分析:(1)作点A关于x轴的对称点A '点,作点C关于x轴的对称点C '点,连接B、A '、C ',连接A A ',由勾股定理不难求出:AC=![]() ,A 'C '=
,A 'C '=![]() ,A 'C=
,A 'C=![]() ,A C '=
,A C '=![]() ,即AC=A 'C ',A 'C=A C ',又因为A A '= A A ',即证明出△AA 'C≌△A 'AC ';
,即AC=A 'C ',A 'C=A C ',又因为A A '= A A ',即证明出△AA 'C≌△A 'AC ';
;(2)作点B关于y轴的对称点,并将其与点C连接起来,连线与y轴的交点即为PB+PC最短时P的位置.
试题解析:
如图,
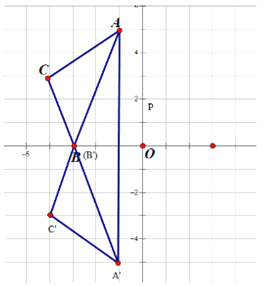
证明:由勾股定理不难求出:AC=![]() ,A 'C '=
,A 'C '=![]() ,A 'C=
,A 'C=![]() ,A C '=
,A C '=![]() ,
,
∴AC=A 'C ',A 'C=A C ',
在△AA 'C和△A 'AC '中,
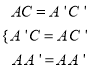 ,
,
∴△AA 'C≌△A 'AC ';
(2)如图,

练习册系列答案
相关题目

