题目内容
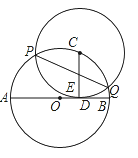
【题目】如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
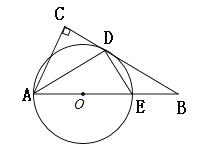
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,
【答案】(1)证明见解析;(2)10.
【解析】
试题(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
试题解析:(1)证明:连接OC;

∵AD平分∠EAC,
∴∠CAD=∠BAD;
又在圆中OA=OD,
∴∠AD0=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD;
则由AE⊥DC知OC⊥DC,
即DC是⊙O的切线.
(2)解:∵∠B=∠B,∠DAE=∠BDE,
∴△BDE∽△BAE,
∴![]() ,
,
∴BD2=BE·BA,
即:BD2=BE·(BE+EA),
∴122=8(8+AE)
∴AE=10.
考点: 1.切线的判定;2.相似三角形的判定与性质.

练习册系列答案
相关题目