题目内容
【题目】四边形![]() 是平行四边形,点
是平行四边形,点![]() 在
在![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() ,
,![]() 重合)
重合)
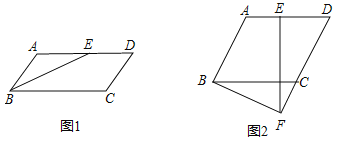
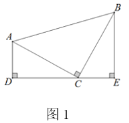
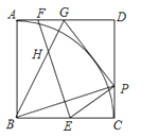
(1)如图1,当点![]() 运动到
运动到![]() 边的中点时,连接
边的中点时,连接![]() ,若
,若![]() 平分
平分![]() ,证明:
,证明:![]() ;
;
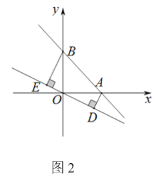
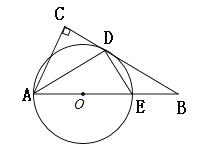
(2)如图2,过点![]() 作
作![]() 且交
且交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得四边形
,使得四边形![]() 是菱形?若存在,请说明当发
是菱形?若存在,请说明当发![]() ,点
,点![]() 分别在线段
分别在线段![]() ,
,![]() 上什么位置时四边形
上什么位置时四边形![]() 是菱形,并证明;若不存在,请说明理由.
是菱形,并证明;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,当![]() 且
且![]() 时,四边形
时,四边形![]() 是菱形,见解析.
是菱形,见解析.
【解析】
(1)由平行四边形的性质和角平分线定义得出∠AEB=∠ABE,证出AB=AE.即可得出结论;
(2)过点A作AH⊥DF于H,由直角三角形的性质得出DH=![]() AD=1,由勾股定理得出AH=
AD=1,由勾股定理得出AH=![]() .在Rt△DEF中,∠EFD=30°,得出DF=2DE=1+
.在Rt△DEF中,∠EFD=30°,得出DF=2DE=1+![]() ,因此FH=DF-DH=
,因此FH=DF-DH=![]() ,得出FH=AB.证出四边形ABFH是平行四边形.由AH=AB,即可得出结论.
,得出FH=AB.证出四边形ABFH是平行四边形.由AH=AB,即可得出结论.
(1)如图(1),平行四边形![]() 中,
中,
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
(2)存在.当![]() 且
且![]() 时,四边形
时,四边形![]() 是菱形.理由如下:
是菱形.理由如下:
如图,过点![]() 作
作![]() 于
于![]() ,
,

在平行四边形![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() .
.
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵在平行四边形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,
∴![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,
∴四边形![]() 是菱形.
是菱形.

练习册系列答案
相关题目