题目内容
【题目】已知
和
，点
在
轴上，若要使
最小，则点的坐标为______.
【答案】
【解析】
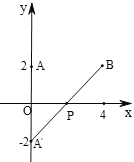
如图，作点A关于x轴是对称点A′，连接BA′，交x轴于点P，根据点A坐标可得点A关于x轴对称的点的坐标为A′（0，-2），根据轴对称的性质可得PA=PA′，即可得BA′是PA+PB的最小值，利用待定系数法可求出直线BA′的解析式，进而可得点P坐标.
如图，作点A关于x轴的对称点A′，连接BA′，交x轴于点P，
∵点A（0，2），
∴点A′（0，-2），
∵点A与点A′关于x轴对称，点P在x轴上，
∴PA=PA′，
∴PA+PB=PB+PA′=BA′，
∴BA′是PA+PB的最小值，
设直线BA′的解析式为y=kx+b，
∴
，
解得：
，
∴直线BA′的解析式为y=x-2，
当y=0时，x=2，
∴点P坐标为（2，0）.
故答案为（2，0）
练习册系列答案
相关题目
【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间，随机对该年级50名学生进行了调查，结果如下表：
时间（天） | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中，众数是 ，中位数是 ；
(2)补全下面的频率分布表和频率分布直方图：
分组 | 频数 | 频率 |
3.5～5.5 | 3 | 0.06 |
5.5～7.5 | 9 | 0.18 |
7.5～9.5 | 0.36 | |
9.5～11.5 | 14 | |
11.5～13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |
(3)请你估算这所学校该年级的学生中，每学期参加社会实践活动时间不少于9天的大约有多少人?
