Question

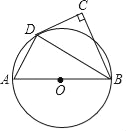
【题目】如图，AB为⊙O的直径，点C在⊙O外，∠ABC的平分线与⊙O交于点D，∠C=90°．

（1）CD与⊙O有怎样的位置关系？请说明理由；

（2）若∠CDB=60°，AB=6，求的长．

Answer 1

【答案】（1）相切，理由见解析；（2）π．

【解析】

（1）连接OD，根据BD是∠ABC的平分线的性质有∠CBD=∠ABD，根据OD=OB，得到∠ODB=∠ABD，等量代换得到∠ODB=∠CBD，根据平行线的判定得到OD∥CB，根据平行线的性质有∠ODC=∠C=90°，即可证明CD与⊙O相切；

（2）根据扇形的弧长公式进行计算即可.

（1）相切．理由如下：

连接OD，

∵BD是∠ABC的平分线，

∴∠CBD=∠ABD，

又∵OD=OB，

∴∠ODB=∠ABD，

∴∠ODB=∠CBD，

∴OD∥CB，

∴∠ODC=∠C=90°，

∴CD与⊙O相切；

（2）若∠CDB=60°，可得∠ODB=30°，

∴∠AOD=60°，

又∵AB=6，

∴AO=3，

∴