题目内容
【题目】根据学习函数的经验，探究函数y＝x2+ax﹣4|x+b|+4（b＜0）的图象和性质：
（1）下表给出了部分x，y的取值；
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知，a＝ ，b＝ ；
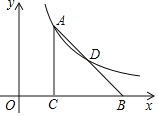
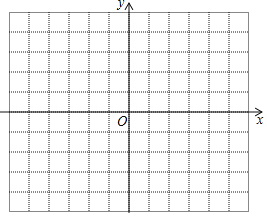
（2）用你喜欢的方式在坐标系中画出函数y＝x2+ax﹣4|x+b|+4的图象；
（3）结合你所画的函数图象，写出该函数的一条性质；
（4）若方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解，请直接写出m的取值范围．
【答案】（1）﹣2，﹣1；（2）详见解析；（3）函数关于x＝1对称；（4）0＜m＜2．
【解析】
（1）将点（0，0）、（1，3）代入函数y＝x2+ax﹣4|x+b|+4，得到关于a、b的一元二次方程，解方程组即可求得；
（2）描点法画图即可；
（3）根据图象即可得到函数关于x＝1对称；
（4）结合图象找，当x＝﹣1时，y＝﹣1；当x＝1，y＝3；则当0＜m＜2时，方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解．
解：（1）将点（0，0）、（1，3）代入函数y＝x2+ax﹣4|x+b|+4（b＜0），得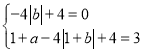
，
解得a＝﹣2，b＝﹣1，
故答案为﹣2，﹣1；
（2）画出函数图象如图：
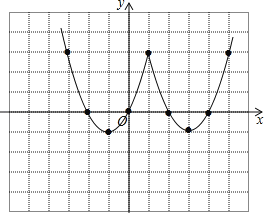
（3）该函数的一条性质：函数关于x＝1对称；
（4）∵方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解
∴二次函数y=x2+ax﹣4|x+b|+4的图像与一次函数y＝x+m至少有三个交点，
根据一次函数图像的变化趋势，
∴当0＜m＜2时，方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解，
故答案为0＜m＜2．
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况，从该校九年级136名女生中，随机抽取了20名女生，进行了1分钟仰卧起坐测试，获得数据如下：
收集数据：抽取20名女生的1分钟仰卧起坐测试成绩(个)如下：
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
（1）整理、描述数据：请你按如下分组整理、描述样本数据，把下列表格补充完整：
范围 |
|
|
|
|
|
|
|
人数 |
(说明：每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
（2）分析数据：样本数据的平均数、中位数、满分率如下表所示：
平均数 | 中位数 | 满分率 |
46.8 | 47.5 |
|
得出结论：①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数；
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下：
平均数 | 中位数 | 满分率 |
45.3 | 49 |
|
请你结合该校样本测试成绩和该区县总体测试成绩，为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估．
