题目内容
已知等腰三角形的两边长分别为5和6,则此三角形的面积为 。
12 或 ;
;
 ;
;试题分析:(1)若两腰长为5,则底边为6,根据勾股定理得高为:
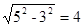 ,
,∴三角形的面积为:
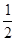 ×6×4=12;
×6×4=12;(2)若两腰长为6,则底边为5,根据勾股定理得高为:
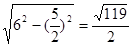 ,
,∴三角形的面积为:
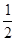 ×5×
×5×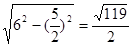 =
= .
.点评:本题关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
题目内容
 ;
;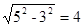 ,
,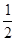 ×6×4=12;
×6×4=12;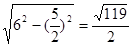 ,
,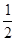 ×5×
×5×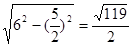 =
= .
.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案