题目内容
【题目】已知一次函数![]() 的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
(1)求一次函数的解析式.
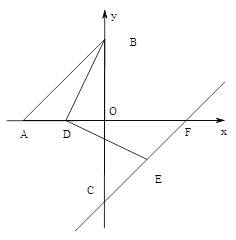
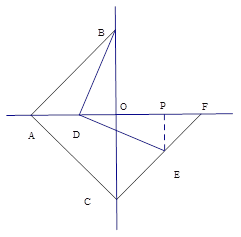
(2)如图,点C与点B关于x轴对称,点D在线段OA上,连结BD,把线段BD顺时针方向旋转90°得到线段DE,作直线CE交x轴于点F,求![]() 的值.
的值.
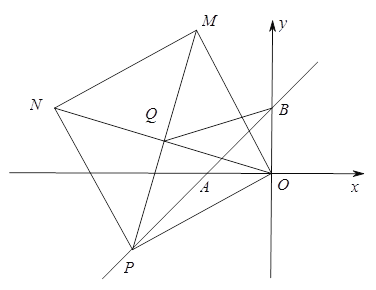
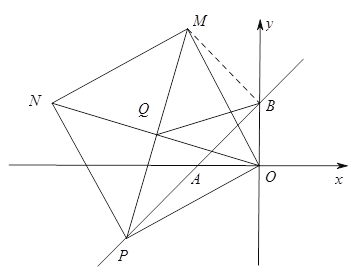
(3)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
【答案】(1)y=x+4.(2)![]() ;(3)不变,
;(3)不变,![]() .
.
【解析】
试题(1)用待定系数法,将M,N两点坐标代入解析式求出k,b即得一次函数解析式;(2)∵点C与点B关于x轴对称,B(0,4),∴C(0,-4),再由旋转性质可得DB=DE,∠BDE=90,过点E作EP⊥x轴于P,易证△BDO≌△DEP,∴OD=PE,DP=BO=4,设D(![]() ,0),则E(
,0),则E(![]() ,
,![]() ),设直线CE解析式是:y=kx+b,把C,E两点坐标代入得:
),设直线CE解析式是:y=kx+b,把C,E两点坐标代入得:![]() ,∴
,∴![]() ,∴CE解析式是y=x-4,∴F(4,0),OC=OF=4,∴PE=PF,∴EF=
,∴CE解析式是y=x-4,∴F(4,0),OC=OF=4,∴PE=PF,∴EF=![]() ,∵A(-4,0),∴DF=4+a,DA=4-a,∴
,∵A(-4,0),∴DF=4+a,DA=4-a,∴![]() =
=![]() =
=![]() =
=![]() ;(3)此题连接BM,因为AO=BO,MO=PO,且∠BOM=∠AOP,得出△BOM≌△AOP(SAS),∵∠PAO=135,∴∠MBP=∠PAO=135,∴∠MBP=90°,在Rt△MBP中,MQ=PQ,∴BQ是此直角三角形斜边中线,等于斜边一半,BQ=
;(3)此题连接BM,因为AO=BO,MO=PO,且∠BOM=∠AOP,得出△BOM≌△AOP(SAS),∵∠PAO=135,∴∠MBP=∠PAO=135,∴∠MBP=90°,在Rt△MBP中,MQ=PQ,∴BQ是此直角三角形斜边中线,等于斜边一半,BQ=![]() MP,MP又是正方形对角线,∴MP=
MP,MP又是正方形对角线,∴MP=![]() OP,∴BQ:OP=
OP,∴BQ:OP=![]() MP:OP=
MP:OP=![]() ×
×![]() OP:OP=
OP:OP=![]() ,∴
,∴![]() 的值不变,是
的值不变,是![]() .
.
试题解析:(1)用待定系数法,将M,N两点坐标代入解析式得:![]() ,解得b=4,k=1,∴一次函数的解析式是y=x+4;(2)∵点C与点B关于x轴对称,B(0,4),∴C(0,-4),再由旋转性质可得DB=DE,∠BDE=90,过点E作EP⊥x轴,易证△BDO≌△DEP,设D(
,解得b=4,k=1,∴一次函数的解析式是y=x+4;(2)∵点C与点B关于x轴对称,B(0,4),∴C(0,-4),再由旋转性质可得DB=DE,∠BDE=90,过点E作EP⊥x轴,易证△BDO≌△DEP,设D(![]() ,0),则E(
,0),则E(![]() ,
,![]() )设直线CE解析式是:y=kx+b,,把C,E两点坐标代入得:
)设直线CE解析式是:y=kx+b,,把C,E两点坐标代入得:![]() ,∴
,∴![]() ∴CE解析式:y=x-4,y=0时,,x=4,∴F(4,0),OC=OF=4,∴PE=PF,∴EF=
∴CE解析式:y=x-4,y=0时,,x=4,∴F(4,0),OC=OF=4,∴PE=PF,∴EF=![]() ,∵A(-4,0),∴DF=4+a,DA=4-a,
,∵A(-4,0),∴DF=4+a,DA=4-a,
∴![]() =
=![]() =
=![]() =
=![]() .∴
.∴![]() 的值是
的值是![]() .
.
(3)连结BM,由正方形性质可得OM=OP,∠MOP=90,由A,B点坐标可得AO=BO,又∵∠BOM=∠AOP(同角的余角相等),可证△BOM≌△AOP(SAS),∴∠MBO=∠PAO=180-45=135°,∴∠MBP=135-45=90°,在Rt△MBP中,MQ=PQ,BQ是此直角三角形斜边中线,等于斜边一半,∴BQ=![]() MP;在Rt△MOP中,,MP=
MP;在Rt△MOP中,,MP=![]() OP;∴BQ:OP=
OP;∴BQ:OP=![]() MP:OP=
MP:OP=![]() ×
×![]() OP:OP=
OP:OP=![]() ,当点P在直线AB上运动时,
,当点P在直线AB上运动时,![]() 的值不变,是
的值不变,是![]() ,∴
,∴![]()

 名校课堂系列答案
名校课堂系列答案