题目内容
如图,在平面直角坐标系中,已知A(8,0),B(0,6),⊙M经过原点O及点A、B.
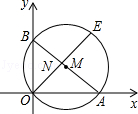
(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线l,求直线l的解析式;
(3)∠BOA的平分线交AB于点N,交⊙M于点E,求点N的坐标和线段OE的长.

(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线l,求直线l的解析式;
(3)∠BOA的平分线交AB于点N,交⊙M于点E,求点N的坐标和线段OE的长.
解:(1)∵∠AOB=90°,∴AB为⊙M的直径。
∵A(8,0),B(0,6),∴OA=8,OB=6。
∴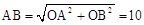 。
。
∴⊙M的半径为5;圆心M的坐标为((4,3)。
(2)如图,设点B作⊙M的切线l交x轴于C,

∵BC与⊙M相切,AB为直径,∴AB⊥BC。
∴∠ABC=90°,∴∠CBO+∠ABO=90°。
∵∠BAO+∠ABO=90°,∴∠BAO=∠CBO。
∴Rt△ABO∽Rt△BCO。
∴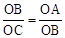 ,即
,即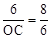 ,解得
,解得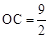 。
。
∴C点坐标为(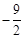 ,0)。
,0)。
设直线BC的解析式为y=kx+b,
把B(0,6)、C点(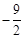 ,0)分别代入得
,0)分别代入得
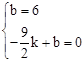 ,解得
,解得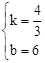 。
。
∴直线l的解析式为y=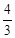 x+6。
x+6。
(3)如图,作ND⊥x轴,连接AE,
∵∠BOA的平分线交AB于点N,∴△NOD为等腰直角三角形。
∴ND=OD。∴ND∥OB。∴△ADN∽△AOB。
∴ND:OB=AD:AO,∴ND:6=(8﹣ND):8,解得ND=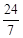 。
。
∴OD=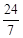 ,ON=
,ON=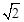 ND=
ND=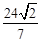 。
。
∴N点坐标为(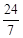 ,
,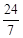 )。
)。
∵△ADN∽△AOB,∴ND:OB=AN:AB,即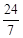 :6=AN:10,解得AN=
:6=AN:10,解得AN=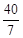 。
。
∴BN=10﹣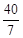 =
=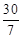 。
。
∵∠OBA=OEA,∠BOE=∠BAE,∴△BON∽△EAN。
∴BN:NE=ON:AN,即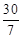 :NE=
:NE=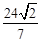 :
: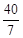 ,解得NE=
,解得NE=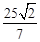 。
。
∴OE=ON+NE=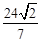 +
+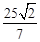 =
=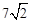 。
。
∵A(8,0),B(0,6),∴OA=8,OB=6。
∴
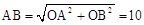 。
。∴⊙M的半径为5;圆心M的坐标为((4,3)。
(2)如图,设点B作⊙M的切线l交x轴于C,

∵BC与⊙M相切,AB为直径,∴AB⊥BC。
∴∠ABC=90°,∴∠CBO+∠ABO=90°。
∵∠BAO+∠ABO=90°,∴∠BAO=∠CBO。
∴Rt△ABO∽Rt△BCO。
∴
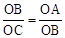 ,即
,即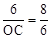 ,解得
,解得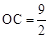 。
。∴C点坐标为(
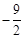 ,0)。
,0)。设直线BC的解析式为y=kx+b,
把B(0,6)、C点(
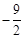 ,0)分别代入得
,0)分别代入得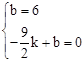 ,解得
,解得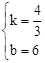 。
。∴直线l的解析式为y=
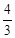 x+6。
x+6。(3)如图,作ND⊥x轴,连接AE,
∵∠BOA的平分线交AB于点N,∴△NOD为等腰直角三角形。
∴ND=OD。∴ND∥OB。∴△ADN∽△AOB。
∴ND:OB=AD:AO,∴ND:6=(8﹣ND):8,解得ND=
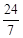 。
。∴OD=
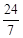 ,ON=
,ON=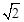 ND=
ND=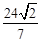 。
。∴N点坐标为(
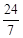 ,
,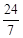 )。
)。∵△ADN∽△AOB,∴ND:OB=AN:AB,即
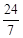 :6=AN:10,解得AN=
:6=AN:10,解得AN=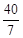 。
。∴BN=10﹣
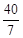 =
=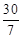 。
。∵∠OBA=OEA,∠BOE=∠BAE,∴△BON∽△EAN。
∴BN:NE=ON:AN,即
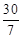 :NE=
:NE=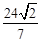 :
: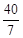 ,解得NE=
,解得NE=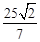 。
。∴OE=ON+NE=
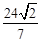 +
+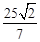 =
=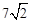 。
。(1)根据圆周角定理∠AOB=90°得AB为⊙M的直径,则可得到线段AB的中点即点M的坐标,然后利用勾股定理计算出AB=10,则可确定⊙M的半径为5。
(2)点B作⊙M的切线l交x轴于C,由切线的性质得AB⊥BC,由等角的余角相等得到∠BAO=∠CBO,根据相似三角形的判定方法有Rt△ABO∽Rt△BCO,所以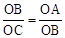 ,可解得
,可解得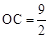 ,则C点坐标为(
,则C点坐标为(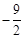 ,0),最后运用待定系数法确定l的解析式。
,0),最后运用待定系数法确定l的解析式。
(3)作ND⊥x轴,连接AE,易得△NOD为等腰直角三角形,所以ND=OD,ON=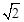 ND,再利用ND∥OB得到△ADN∽△AOB,则ND:OB=AD:AO,即ND:6=(8﹣ND):8,解得ND=
ND,再利用ND∥OB得到△ADN∽△AOB,则ND:OB=AD:AO,即ND:6=(8﹣ND):8,解得ND=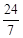 ,所以OD=
,所以OD=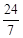 ,ON=
,ON=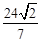 ,即可确定N点坐标;由于△ADN∽△AOB,利用ND:OB=AN:AB,可求得AN=
,即可确定N点坐标;由于△ADN∽△AOB,利用ND:OB=AN:AB,可求得AN=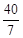 ,则BN=10﹣
,则BN=10﹣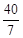 =
=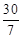 ,然后利用圆周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出ME,最后由OE=ON+NE计算即可。
,然后利用圆周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出ME,最后由OE=ON+NE计算即可。
(2)点B作⊙M的切线l交x轴于C,由切线的性质得AB⊥BC,由等角的余角相等得到∠BAO=∠CBO,根据相似三角形的判定方法有Rt△ABO∽Rt△BCO,所以
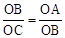 ,可解得
,可解得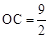 ,则C点坐标为(
,则C点坐标为(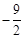 ,0),最后运用待定系数法确定l的解析式。
,0),最后运用待定系数法确定l的解析式。(3)作ND⊥x轴,连接AE,易得△NOD为等腰直角三角形,所以ND=OD,ON=
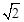 ND,再利用ND∥OB得到△ADN∽△AOB,则ND:OB=AD:AO,即ND:6=(8﹣ND):8,解得ND=
ND,再利用ND∥OB得到△ADN∽△AOB,则ND:OB=AD:AO,即ND:6=(8﹣ND):8,解得ND=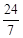 ,所以OD=
,所以OD=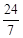 ,ON=
,ON=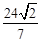 ,即可确定N点坐标;由于△ADN∽△AOB,利用ND:OB=AN:AB,可求得AN=
,即可确定N点坐标;由于△ADN∽△AOB,利用ND:OB=AN:AB,可求得AN=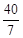 ,则BN=10﹣
,则BN=10﹣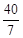 =
=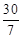 ,然后利用圆周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出ME,最后由OE=ON+NE计算即可。
,然后利用圆周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出ME,最后由OE=ON+NE计算即可。
练习册系列答案
相关题目

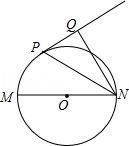
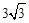 ,求NQ的长.
,求NQ的长.
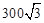 米,则这段弯路的长度为
米,则这段弯路的长度为