题目内容
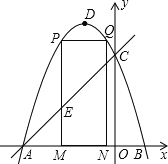
【题目】如图，抛物线y=-x2-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．
（1）求A、B、C的坐标；
（2）设点H是第二象限内抛物线上的一点，且△HAB的面积是6，求点H的坐标；
（3）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积．
【答案】（1）A（-3，0），B（1，0），C（0，3）；（2）H（-2，3）；（3）
．
【解析】
试题分析：（1）通过解析式即可得出C点坐标，令y=0，解方程得出方程的解，即可求得A、B的坐标．
（2）根据AB的长和三角形面积求得H的纵坐标为3，代入解析式即可求得横坐标；
（3）设M点横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，矩形PMNQ的周长d=-2m2-8m+2，将-2m2-8m+2配方，根据二次函数的性质，即可得出m的值，然后求得直线AC的解析式，把x=m代入可以求得三角形的边长，从而求得三角形的面积．
试题解析：（1）由抛物线y=-x2-2x+3可知，C（0，3），
令y=0，则0=-x2-2x+3，解得x=-3或x=1，
∴A（-3，0），B（1，0）．
（2）∵A（-3，0），B（1，0）．
∴AB=4，
∵△HAB的面积是6，点H是第二象限内抛物线上的一点，
∴H的纵坐标为3，
把y=3代入y=-x2-2x+3得3=-x2-2x+3，解得x1=0，x2=-2，
∴H（-2，3）；
（3）由抛物线y=-x2-2x+3可知，对称轴为x=-1，
设M点的横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，
∴矩形PMNQ的周长=2（PM+MN）=（-m2-2m+3-2m-2）×2=-2m2-8m+2=-2（m+2）2+10，
∴当m=-2时矩形的周长最大．
∵A（-3，0），C（0，3），设直线AC解析式为y=kx+b，
则
解得：
，
∴解析式y=x+3，当x=-2时，则E（-2，1），
∴EM=1，AM=1，
∴S=×AM×EM=．
