题目内容
【题目】如图1，△ABC的边BC的中垂线DM交∠BAC的平分线AD于D， DE⊥AB于点E，DF⊥AC于F.连接DB、DC
（1）求证：△DBE≌△DFC.
（2）求证：AB+AC=2AE
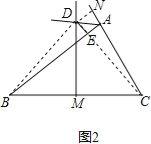
（3）如图2，若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D， DE⊥AB于点E，且AB>AC，写出AE、BE、AC之间的等量关系。（不需证明，只需在图2中作出辅助线、说明证哪两个三角形全等即可）。
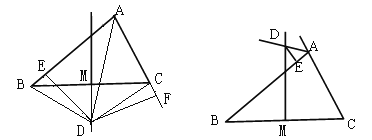
图1 图2
【答案】（1）见解析（2）见解析（3）BE=AE+AC
【解析】试题分析：（1）根据线段垂直平分线的性质得到DB=DC，根据角平分线的性质得到DE=DF，由全等三角形的判定定理即可得到结论；
（2）根据全等三角形的性质得到AE=AF，BE=CF，等量代换即可得到结论；
（3）如图2，过D作DN⊥AC，垂足为N，连接DB、DC，根据线段垂直平分线的性质和角平分线的性质得到DN=DE，DB=DC，推出Rt△DBE≌Rt△DCN（HL），根据全等三角形的性质得到BE=CN，由于Rt△DEA≌Rt△DNA（HL），根据全等三角形的性质得到AN=AE，等量代换即可得到结论．
（1）证明：∵DM垂直平分BC，
∴DB=DC，
∵∠1=∠2，DE⊥AB，DF⊥AC，
∴DE=DF，
在Rt△DEB与Rt△DFC中，
，
∴Rt△DEB≌Rt△DFC；
（2）∵∠AED=∠AFD=90°，
在Rt△ADE≌Rt△ADF中，
，
∴Rt△ADE≌Rt△ADF（HL），
∴AE=AF，
又∵Rt△DEB≌Rt△DFC，
∴BE=CF，
∴AB+AC=AE+BE+AF﹣CF=2AE；
（3）BE=AE+AC．
证明：如图2，过D作DN⊥AC，垂足为N，连接DB、DC，
则DN=DE，DB=DC，
又∵DE⊥AB，DN⊥AC，
∴∠DEB=∠DNC=90°，
在Rt△DBE和Rt△DCN中，
，
∴Rt△DBE≌Rt△DCN（HL）
∴BE=CN，
在Rt△DEA和Rt△DNA中，
，
∴Rt△DEA≌Rt△DNA（HL），
∴AN=AE，
∴BE=AC+AN=AC+AE，
即BE=AE+AC．
