题目内容
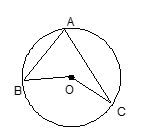
如图,△ABC的3个顶点都在⊙O上,AD是△ABC的高,AE是圆的直径,AB=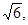 AC=
AC=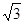 ,AD=
,AD=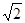 ,则圆的半径是
,则圆的半径是 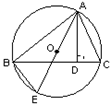
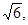 AC=
AC=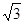 ,AD=
,AD=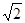 ,则圆的半径是
,则圆的半径是 
1.5
设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,△ACD∽△AEB,利用相似三角形的对应边成比例即可求解.
解答:解:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,
∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADE=90°,
∴△ACD∽△AEB,
∴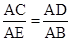 ,
,
即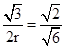 ,
,
解得r=1.5.
故答案为:1.5.
解答:解:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,
∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADE=90°,
∴△ACD∽△AEB,
∴
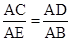 ,
,即
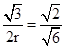 ,
,解得r=1.5.
故答案为:1.5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,DE=
,DE= ,下列中图象中,能表示
,下列中图象中,能表示

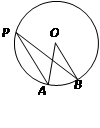


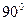 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
 ,求⊙O的直径BC.
,求⊙O的直径BC.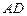 为
为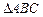 外接圆的直径,
外接圆的直径,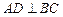 ,垂足为点
,垂足为点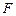 ,
,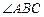 的平分线交
的平分线交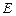 ,连接
,连接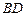 ,
,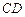 .
.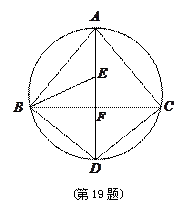
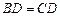 ;
; 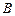 ,
,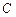 三点是否在以
三点是否在以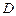 为圆心,以
为圆心,以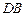 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.