Question

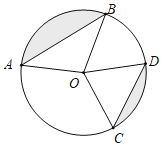
【题目】如图，已知⊙O的半径为5，弦AB=8，CD=6，则图中阴影部分面积为（ ）

A. π–24 B. 9π C. π–12 D. 9π–6

Answer 1

【答案】A

【解析】

过点O作OE⊥AB于E，作OF⊥CD于F，根据垂径定理求出AE、CF，再利用勾股定理列式求出OE=OF，从而得到AE=OF，OE=CF，然后利用“边角边”证明△AOE和△OCF全等，根据全等三角形对应角相等可得∠AOE=∠OCF，再求出∠AOE+∠COF=90°，然后求出∠AOB+∠COD=180°，把弧CD旋转到点D与点B重合，构建直角三角形ABC；然后根据圆的面积公式和直角三角形的面积公式来求阴影部分的面积：阴影面积=半圆面积-直角三角形ABC的面积．

解：如图1，过点O作OE⊥AB于E，作OF⊥CD于F，

由垂径定理得，AE=AB=×8=4，CF=CD=×6=3，

由勾股定理得，OE===3，

OF===4，

∴AE=OF，OE=CF，

在△AOE和△OCF中，，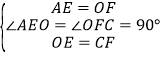

∴△AOE≌△OCF（SAS），∴∠AOE=∠OCF，

∵∠OCF+∠COF=90°，∴∠AOE+∠COF=90°，

∴∠AOB+∠COD=2（∠AOE+∠COF）=2×90°=180°，

如图2把弧CD旋转到点D与点B重合．

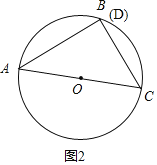
∴△ABC为直角三角形，且AC为圆的直径；

∵AB=8，CD=6，∴AC=10（勾股定理），

∴阴影部分的面积=S半圆–S△ABC=π×52–×6×8=π–24；

故选A．